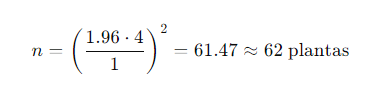Temas de guia para la unidad 1.- Estimación

1.3 Intervalos de Confianza para la Media

1.3.1 Con Distribución Normal

Fórmula del Intervalo de Confianza para la Media con Distribución Normal

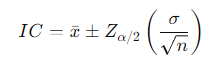
Donde:

$\bar{x}$ : Media muestral.
$Z_{\alpha/2}$ : Valor crítico de la distribución normal estándar para un nivel de confianza $(1 - \alpha)$ .
$\sigma$ : Desviación estándar de la población.
$n$ : Tamaño de la muestra.

Enlace de como utilizar la tabla de distibucion normal (Z alfa medios).

Enlace para entender mejor la aplicacion de los calculos de distribucion normal.

1.3.2 Con Distribución "t" de Student

Fórmula del Intervalo de Confianza para la Media con Distribución "t"

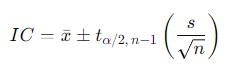
Donde:

$t_{\alpha/2, \, n-1}$ : Valor crítico de la distribución "t" de Student con $n-1$ grados de libertad.
s: Desviación estándar muestral.

ejemplo:

Ejercicio 3: Intervalo de Confianza con Distribución Normal

En una investigación sobre el rendimiento de las plantas de tomate, se encontró que la media muestral es de 2.5 kg/planta con una desviación estándar poblacional conocida de 0.5 kg. Si se selecciona una muestra de 36 plantas, calcula el intervalo de confianza al 95%.

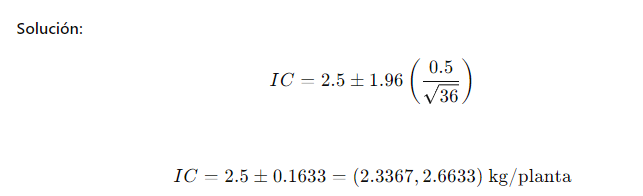
1.3.1 Determinación del Tamaño de Muestra con Grado de Confianza y Estimación de μ

Fórmula para el Tamaño de Muestra

n = {(\frac{Z_{α / 2} \cdot σ}{E})}^{2}

Donde:

$E$ : Margen de error permitido.

Ejercicio 4: Determinación del Tamaño de Muestra

Para estimar la altura media de las plantas de soya con un margen de error de 1 cm y un nivel de confianza del 95%, y con una desviación estándar conocida de 4 cm, determina el tamaño mínimo de la muestra.

Solución: