3.1 REGLA GENERAL PARA DERIVAR DIVERSAS TIPOS DE FUNCIONES
1. LA DERIVADA
Introducción
En este capítulo vamos a investigar cómo varía
el valor de una función al variar la variable independiente. El problema fundamental del Cálculo diferencial es el de establecer con toda
precisión una medida de esta variación. La investigación de problemas
de esta índole, problemas que trataban de magnitudes que variaban de
una manera continua, llevó a Newton * al descubrimiento de los prin
cipios fundamentales del Cálculo infinitesimal, el instrumento científico
más poderoso del matemático moderno.
Incrementos
El incremento de una variable que pasa de un
valor numérico a otro es la diferencia que se obtiene restando el valor
inicial del valor final. Un incremento de x se representa por el símbolo Δx, que se lee "delta x' '. El estudiante no debe leer este símbolo "delta veces x".
Es evidente que el incremento puede ser positivo o negativo, **
según que la variable aumente o disminuya al cambiar de valor.
Asimismo

Si en y = f (x) la variable independiente x toma un incremento Δx ,
entonces Δy indicará el incremento correspondiente de la función f (x)
(o sea, de la variable dependiente y).
El incremento Δy siempre ha de contarse desde el valor inicial defi
nido de y, que corresponde al valor inicial arbitrariamente fijado de x
desde el cual se cuenta el incremento Δx. Por ejemplo, consideremos
la función:
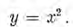
Si tomamos x = 10 como valor inicial de x, esto fija y = 100
corno valor inicial de y.

En este ejemplo, Y aumenta cuando X aumenta, y Y decrece cuando x decrece. Los valores correspondientes de Δx y Δy tienen un mismo signo. Puede acontecer que y decrezca cuando x aumenta, o viceversa; Δx y Δy tendrán entonces signos contrarios.
Comparación de incrementos
Consideremos la función 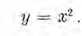
Supongamos que x tiene un valor inicial fijo y le damos después un
incremento Δx . Entonces y tomará un incremento correspondiente Δy,
y tendremos:
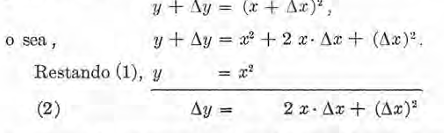
Obtenemos el incremento Δy en función de x y Δx.
Para hallar la razón de los incrementos, basta dividir los dos
miembros de (2) por Δx, y resulta:
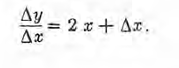
Si el valor de x es 4, entonces: 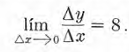
Observemos ahora con cuidado, mediante una tabla, cómo se
comporta la razón de los incrementos de x y de y cuando el incremento de x decrece.
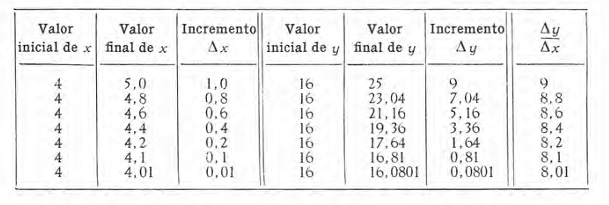
Esta tabla pone de manifiesto que al decrecer Δx también disminuye Δy, mientras que la razón de los dos incrementos toma los
valores sucesivos 9, 8,8, 8,6, 8,4, 8,2, 8,1, 8,01. Esta sucesión
de valores nos dice que podemos hacer que el valor de la razón 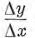 sea
Luego,
tan próximo a 8 comno deseemos con sólo tomar a Δx suficientemente pequeño. Luego
sea
Luego,
tan próximo a 8 comno deseemos con sólo tomar a Δx suficientemente pequeño. Luego
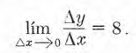
¿Qué es la derivada? El concepto gráfico de derivada. ¿Qué es doblegar la curva?
Derivada de una función de una variable
La derivada * de una función es el límite de la razón del incremento
de la función al incremento de la variable independiente cuando éste
tiende a cero.
Cuando el límite de esta razón existe , se dice que la función es
derivable o que tiene derivada.
La definición puede darse mediante símbolos, en la forma siguiente:
1. Dada la función 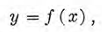 consideremos un valor inicial fijo de x
consideremos un valor inicial fijo de x
2. Demos a x un incremento Δx; entonces obtenernos para la función
y un incremento Δy, siendo el valor final de la función.
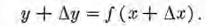
3. Para hallar el incremento de la función, restarnos (1) de (2); se
obtiene:
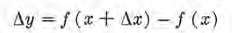
4. Dividiendo los dos miembros por Δx, incremento de la variable
independiente, resulta:

El límite del segundo miembro cuando 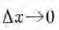 es, por definición,
la derivada de f( x), o sea, según (1), de y, y se representa por el símbolo
es, por definición,
la derivada de f( x), o sea, según (1), de y, y se representa por el símbolo 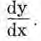 Luego, la igualdad
Luego, la igualdad
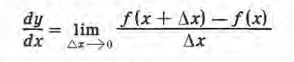
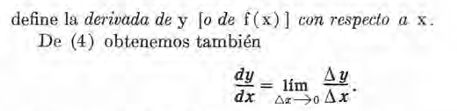

Símbolos para representar las derivadas.
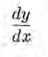
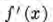
Si y = f(x), podemos escribir la igualdad 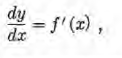 que se lee "la derivada de y con respecto a x es igual a f prima
de x"
El símbolo
que se lee "la derivada de y con respecto a x es igual a f prima
de x"
El símbolo 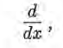
considerado por sí mismo, se llama operador derivada; indica que toda
función que se escriba después de él ha de derivarse con respecto
a x. Así,

Regla general para la derivación
PRIMER PASO. Se sustituye en la función x por x + Δx, y se calcula el nuevo valor de la función y + Δy .
SEGUNDO PASO . Se resta el valor dado de la función del nuevo valor y se obtiene Δy ( incremento de la función ).
TERCER PASO. Se divide Δy (incremento de la función) por Δx (incremento de la variable independiente).
CUARTO PASO. Se calcula el límite de este cociente cuando Δx
( incremento de la variable independiente) t'iende a cero. El límite así
hallado es la derivada buscada.
EJEMPLO 1. Hallar la derivada de la función 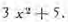
Resolución. Aplicando los pasos sucesivos de la regla general, obtenemos,
después de hacer
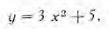
Primer paso 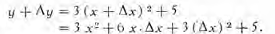
Segundo paso 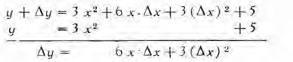
Tercer paso 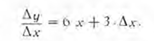
Cuarto paso 
EJEMPLO 2. Hallar la derivada de 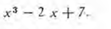
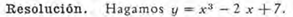
Primer paso 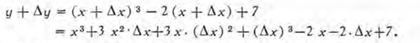
Segundo paso 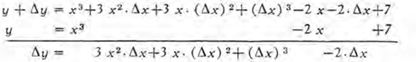
Tercer paso 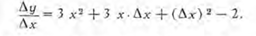
Cuarto paso 