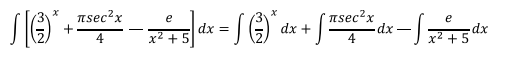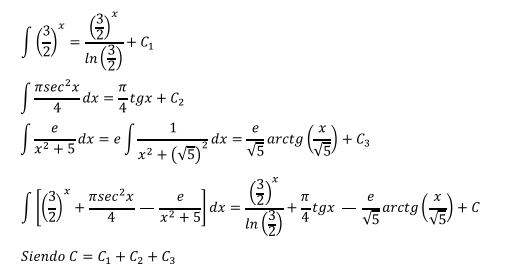1.1 INTEGRAL INDEFINIDA

1. INTEGRAL INDEFINIDA

El Cálculo fue desarrollado para resolver problemas como encontrar la pendiente de una curva en un punto, o el área bajo ella, la velocidad de un cuerpo en un cierto instante sabiendo la distancia, o caso contrario, sabiendo la velocidad, encontrar la distancia recorrida. Estas fueron una de las muchas aplicaciones por la que científicos como Issac Newton (1643-1727) o Gottfried Leibniz (1646-1716) desarrollaron el Cálculo Integral y el Cálculo Diferencial.

En la actualidad, el Cálculo Diferencial y el Cálculo Integral constituyen materias obligatorias en cualquier carrera de Ingeniería por ser herramientas poderosas para resolver problemas de aplicación en la ingeniería e incluso en otras disciplinas como la Biología o la Economía.

Antiderivada y Constante de Integración

A estas alturas de su formación, el estudiante de ingeniería ya está familiarizado con operaciones contrarias como la suma y resta, la multiplicación y división, la potenciación y la radicación. Igual de opuestas constituyen las operaciones de Diferenciación e Integración.

En Cálculo Diferencial vimos que la derivada de una función f se la expresaba como f’ y era otra función que se la podía representar como g, es decir,

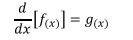
que si la escribimos como diferencial, queda como

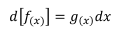
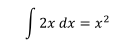
Así, para el primer ejemplo donde la función original era 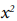 y la función a integrar era 2x:

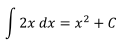
y para regresar a la función original hacemos C=0 

Para el segundo caso

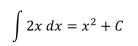
y para regresar a la función original hacemos C=3

Como se puede apreciar, C puede tomar cualquier valor formando una familia de curvas. Esto se puede representar gráficamente como se muestra en la figura 1.

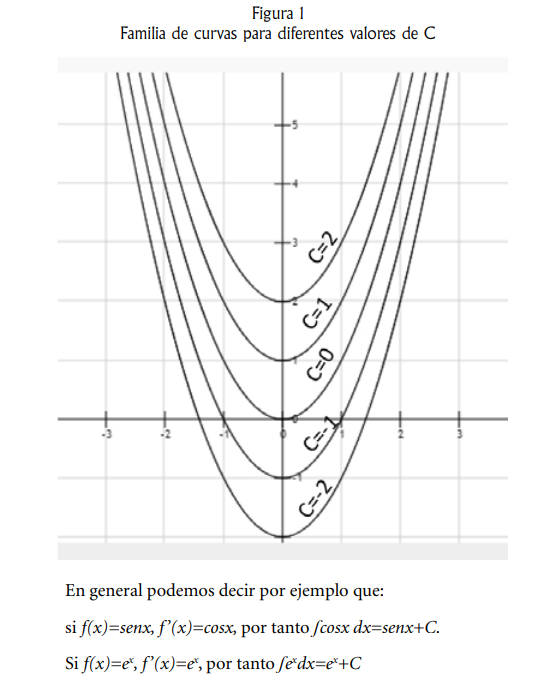
Integración de Formas Elementales

Como ya se dijo, integrar es el proceso contrario a derivar. En la tabla 1 que se muestra a continuación, hay algunas fórmulas que sirven para integrar directamente.

Ejercicio 1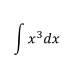              

Solución: En este caso, aplicamos la fórmula 2 de la Tabla 1 haciendo n=3

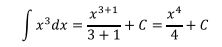
Comprobación: Derivando el resultado se debe regresar a la integral original

Ejercicio 2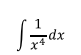   

Solución: Aplicamos la misma fórmula del ejercicio anterior, esta vez haciendo n= -4

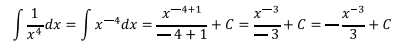
Comprobación

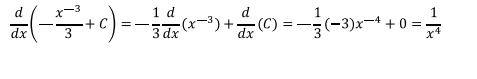
Ejercicio 3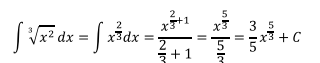  

Comprobación: Se la deja al estudiante

Ejercicio 4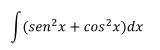    

Aplicando la identidad trigonométrica mencionada se llega a la integral original

                            Tabla 1 Tabla de integrales básicas

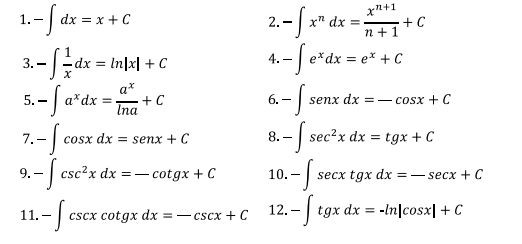
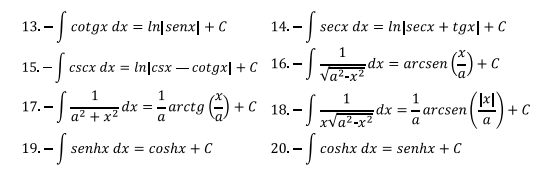
Existen dos propiedades muy usadas en la solución de ejercicios de cálculo integral que son:

Propiedad 1.1

El integral de las suma o resta de dos más funciones es igual a la suma o resta de la integral de cada una de esas funciones.

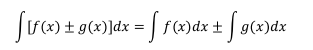
Propiedad 1.2

El integral de la multiplicación de una constante por una función es igual a la multiplicación de dicha constante por el integral de la función.

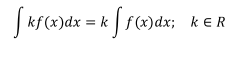
Ejercicio 1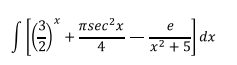  

Aplicando la propiedad 1.1 la integral anterior podemos descomponerla en tres integrales más sencillas