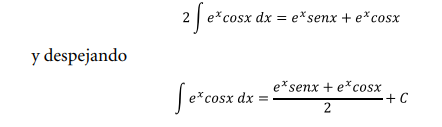2.1 MÉTODOS DE INTEGRACIÓN E INTEGRAL INDEFINIDA

3. 2.3 TÉCNICAS DE INTEGRACIÓN: INTEGRACIÓN POR PARTES

              Integración por partes 

Si el método de cambio de variables no da resultado, otro método que se puede usar es el de integración. Este método se basa en la fórmula para diferenciación de un producto de funciones. 

Sean u y v dos funciones derivables, entonces la diferenciación del producto de esas dos funciones es:

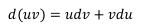
Despejando el primer término del lado derecho de la ecuación,

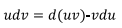
Integrando ambos lados de la ecuación,

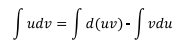
Ya que la integración y la diferenciación son dos procesos inversos, el primer término del lado derecho de la ecuación queda como el producto de las funciones u y v,

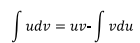
que es la fórmula que se usa en el método de Integración por Partes.

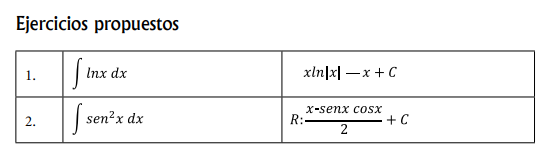
Ejercicio 1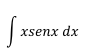  

El éxito de este método en muchos casos se basa en la elección apropiada de que cosa es u y que cosa es dv.

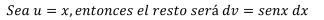
Para aplicar la fórmula se necesitará calcular v y du. Para calcular v se integra dv y para calcular du se halla la diferencial de u.

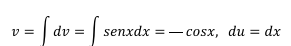
A estas alturas del curso, más de un estudiante se preguntará por qué al integrar v no se tomó en cuenta la constante de integración C. 

Como se hizo anteriormente, esa constante será tomada en cuenta como una sola al final del ejercicio. 

Usando la fórmula de integración por partes,

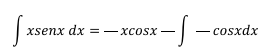
Volviendo a integrar

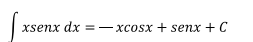
Ejercicio 2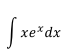 

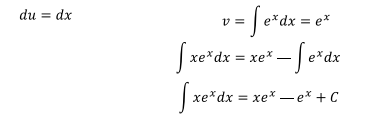
Ejercicio 3  

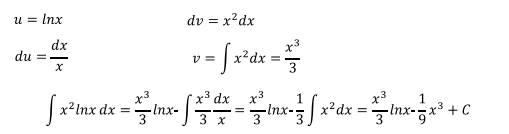
En ocasiones el método de integración por partes hay que aplicarlo varias veces hasta llegar a la respuesta.

Ejercicio 4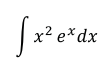  

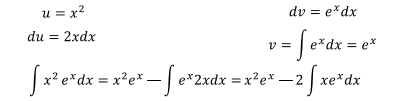
La segunda integral es la misma del ejercicio 2, usando entonces este resultado se tiene

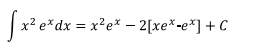
Ejercicio 5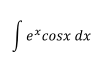  

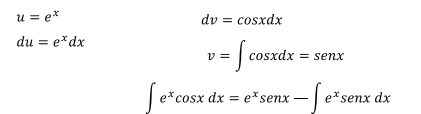
Aplicando nuevamente el método de integración por partes

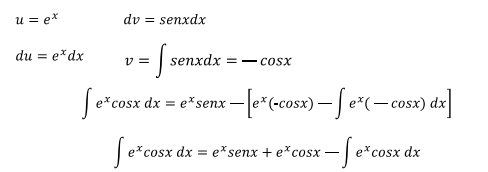
Ya que el integral del lado derecho de la ecuación es igual que el del lado derecho, se puede pasar al lado izquierdo