2.1 MÉTODOS DE INTEGRACIÓN E INTEGRAL INDEFINIDA

4. 2.4 TÉCNICAS DE INTEGRACIÓN: INTEGRACIÓN DE FUNCIONES TRIGONOMÉTRICAS

           Integración de funciones trigonométricas

En este punto el estudiante ya puede reconocer cuando integrar usando sustitución o cambio de variable y cuando usar el método de múltiple integración o por partes. 

Es conveniente que ahora, el estudiante repase sus conocimientos sobre trigonometría, pues el uso de identidades es constante en esta sección y en adelante.

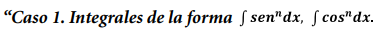
Cuando los integrales tienen esta forma, pueden presentarse dos casos: que n sea par o que n sea impar.

Ejercicio 1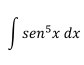 

En este caso el exponente es impar, usar entonces la segunda recomendación

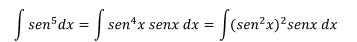
Usando la identidad trigonométrica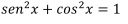 

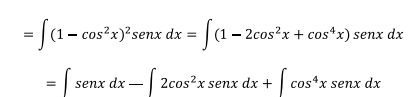
Sustituyendo u=cosx en los dos últimos integrales, du=-senxdx

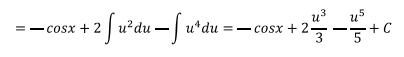
Retornando a la variable original

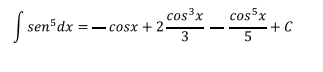
Ejercicio 2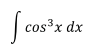  

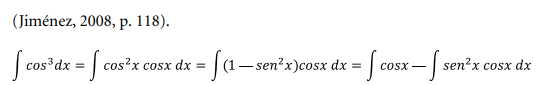
La primera integral es directa. La segunda integral se la resuelve por sustitución o cambio de variable.

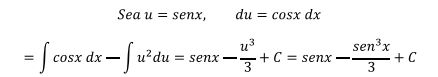
Ejercicio 3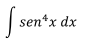  

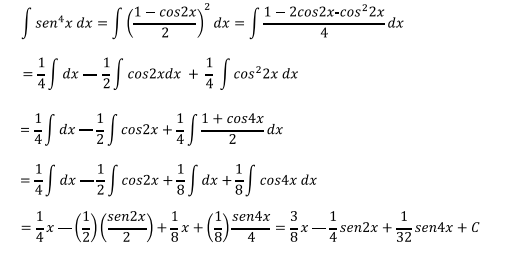
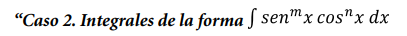
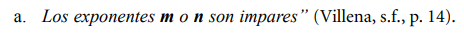
Ejercicio 1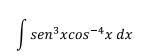  

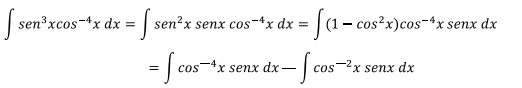
Cambiando de variable

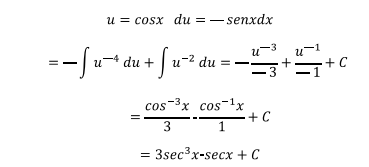
Ejercicio 2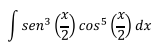  

Reordenando para que el estudiante vea con mayor claridad el proceso se tiene

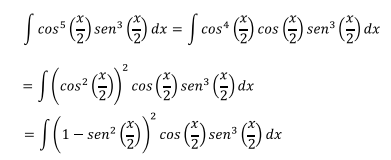
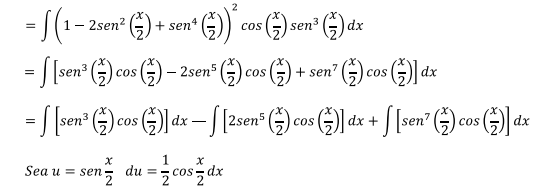
Multiplicando y dividiendo al mismo tiempo por 2 a cada integral con la intención de obtener el valor completo de du en la integral

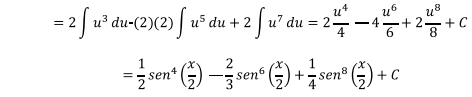
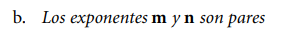
Ejercicio 1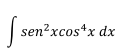  

Ya que ambos exponentes son pares, el procedimiento recomendado es el siguiente:

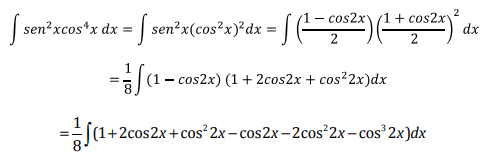
Esta integral ya fue resuelta en el ejercicio 2 del Caso 1 con la diferencia que ahora se trata de ángulo doble. Se deja al estudiante para que resuelva esta parte del ejercicio.

La respuesta final es

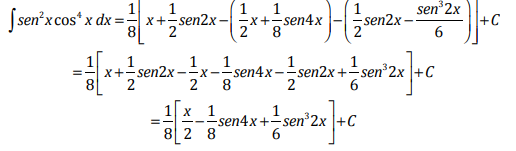
Para estos casos se recomienda usar las identidades de ángulo múltiple y de ángulo negativo que se muestran a continuación:

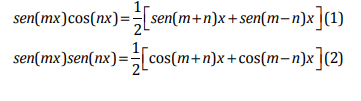
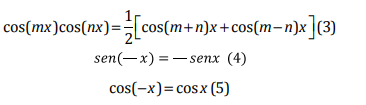
Ejercicio 1  

Aplicando la identidad (1) en donde m=2 y n=4

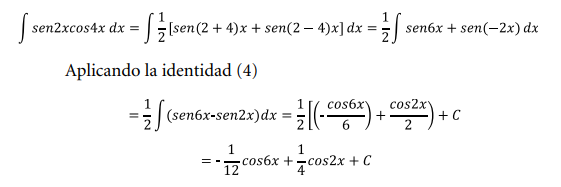
Ejercicio 2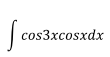  

Aplicando la identidad (3) haciendo m=3 y n=1  

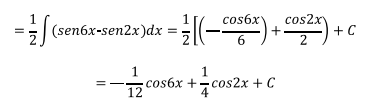
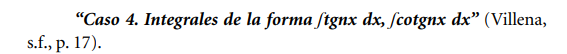
Igual que en los casos anteriores, para llevar estas integrales a una forma donde pueda aplicarse el método de sustitución o cambio de variable, se recomienda usar las siguientes identidades:

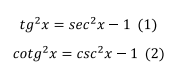
Ejercicio 1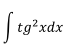  

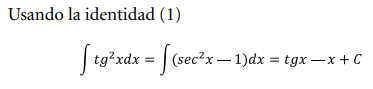
Ejercicio 2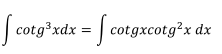  

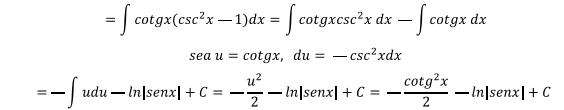
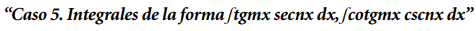
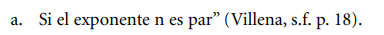
Ejercicio 1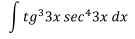  

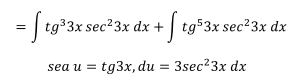
Multiplicando y dividiendo para 3 ambas integrales para tener el diferencial completo

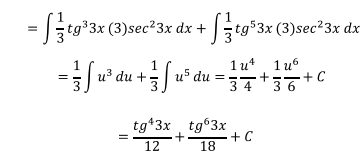
Ejercicio 1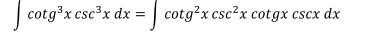   

Usando la identidad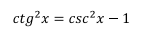   

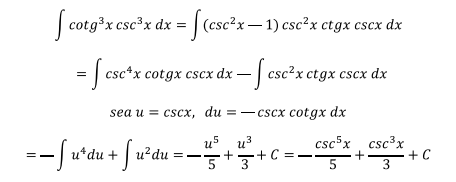
Los casos aquí expuestos cubren una gran cantidad de integrales de combinaciones de funciones trigonométricas, sin embargo puede haber otros casos en donde probablemente se puedan integrar aplicando alguno de los métodos ya vistos.