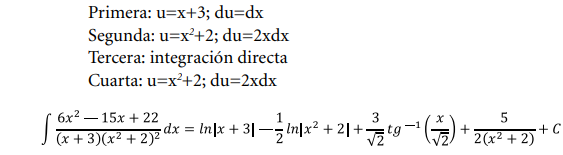2.1 MÉTODOS DE INTEGRACIÓN E INTEGRAL INDEFINIDA
6. 2.6 TÉCNICAS DE INTEGRACIÓN: DE FUNCIONES RACIONALES POR FRACCIONES PARCIALES
Integración de funciones racionales por medio de fracciones parciales
Una función racional está formada por el cociente de dos funciones polinómicas con exponentes enteros (no negativos ni fraccionarios), es decir tienen la forma siguiente:
El grado de un polinomio está dado por el exponente de mayor valor de la variable. Una fracción racional puede ser propia o impropia.
Una fracción es impropia si el grado del polinomio del numerador es mayor o igual que el grado del polinomio del denominador, caso contrario, la fracción es propia.
El método que más adelante se explicará funciona con fracciones racionales propias, de tal manera que si se tiene una fracción racional impropia, es necesario hacer la división del polinomio para poder trabajar con la fracción propia.
Por ejemplo, la siguiente fracción impropia se convierte en la siguiente fracción propia al hacer la división correspondiente.
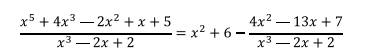
(Se recomienda al estudiante que repase este material antes de continuar con el tema).
Los dos primeros términos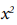 
y 6 son fáciles de integrar y el problema se reduce a integrar la fracción restante.
Antes de aplicar el método, es necesario descomponer el denominador en factores simples de tal manera de aplicar alguno de los siguientes casos:
“Caso 1. Factores lineales distintos. A cada factor lineal ax+b,
del denominador de una fracción racional propia, le corresponde una
fracción de la forma
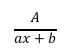
siendo A una constante a determinar”. (Ayres, 1989, p. 150)
Caso 2. Factores lineales iguales. A cada factor lineal ax+b que
figure n veces en el denominador de una fracción racional propia, le
corresponde una suma de n fracciones de la forma
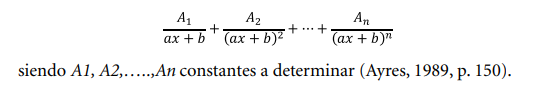
Caso 3. Factores cuadráticos distintos. A cada factor cuadrático
reducible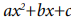 
que figure en el denominador de una fracción propia, le corresponde una fracción de la forma
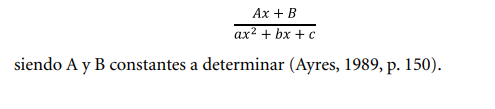
Caso 4. Factores cuadráticos iguales. A cada factor cuadrático
irreducible,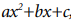 
que se repita n veces en el denominador de una
fracción racional propia, le corresponde una suma de n fracciones de la
forma
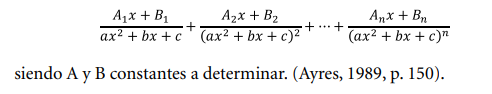
Ejercicio 1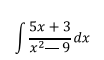 
El integrando es una función racional propia, ya que el máximo exponente en el numerador es 1 mientras que el máximo exponente del denominador es 2.
El denominador de esta fracción se lo puede descomponer en la
siguiente manera:
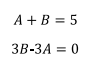
Multiplicando la primera ecuación por 3 y sumado con la segunda ecuación
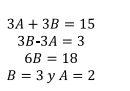
El integral original se convierte entonces en
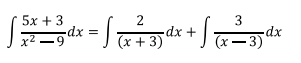
Estas dos integrales pueden ser fácilmente resueltas usando sustitución de variables haciendo:
Ejercicio 2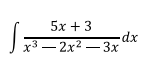 
Esta es una fracción racional propia que se la puede factorizar de
la siguiente forma:
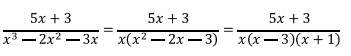
Como se tienen 3 factores lineales diferentes, se aplica el caso 1.
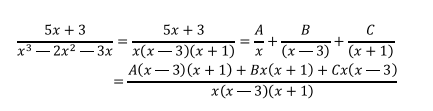
Ya que los denominadores evidentemente son iguales, nos vamos
a centrar en los numeradores
Agrupando los términos con x2
, los que tiene x y los independientes se tiene:
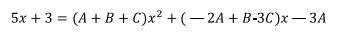
Comparando los términos se forman las siguientes ecuaciones:
Resolviendo este sistema de 3 ecuaciones con 3 incógnitas se tiene:
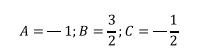
Una manera más rápida de encontrar los valores de A, B y C es
la siguiente:
Ejercicio 3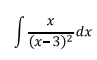 
Ejercicio 4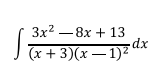 
Como se puede apreciar, se tiene una mezcla del primero y segundo caso, por tanto
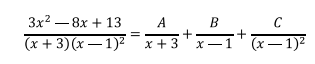
Trabajando sobre el numerador, ya que evidentemente los denominadores son iguales se tiene:
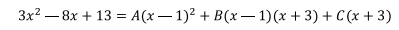
Seleccionando, como se hizo en la segunda parte del ejercicio 2,
los números x=1; x=-3; x=0 en donde x=0 se lo escoge por comodidad,
se tiene:
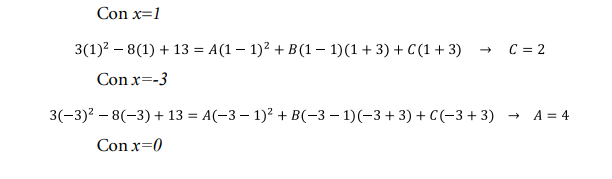
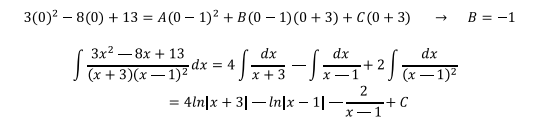
Ejercicio 5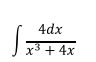 
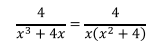
En este se tiene una combinación del primer caso y el tercero, ya
que entre paréntesis se tiene un factor cuadrático. La expresión anterior
queda entonces como sigue:
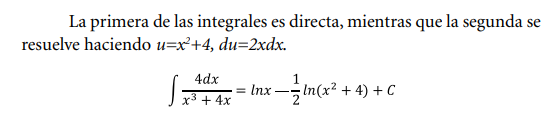
Ejercicio 6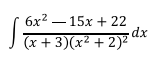 
Esta es una combinación del caso 1 y el caso 4
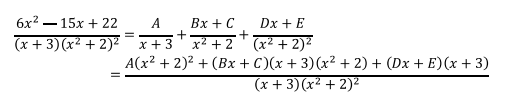
Comparando numeradores
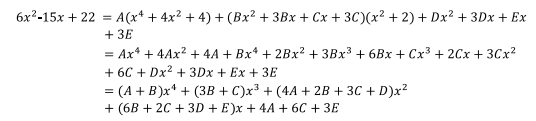
Igualando términos salen las 5 ecuaciones que se necesitan para
encontrar las 5 incógnitas
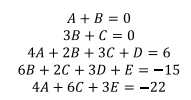
En este punto lo mejor para encontrar las 5 variables es usar calculadoras de sistemas de ecuaciones o cualquiera de los métodos enseñados en Álgebra Lineal. En este caso, a manera de recordatorio se usará
el método de Cramer.
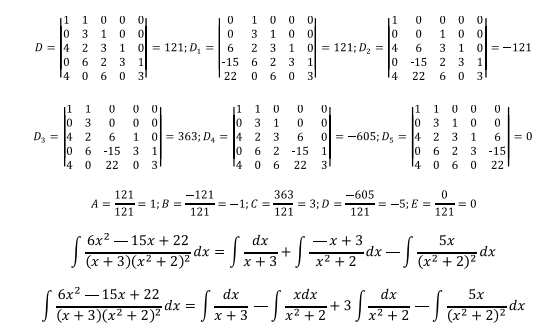
Sustituciones recomendadas para la solución de las cuatro integrales:
