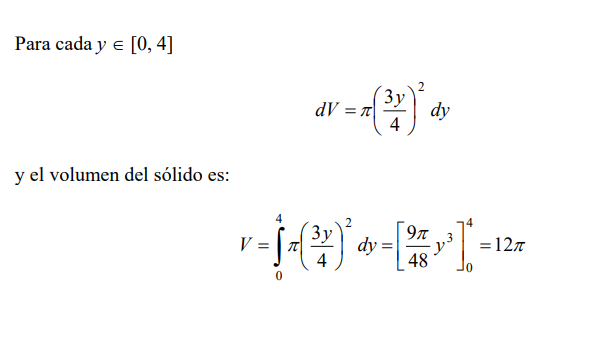3.1 APLICACIONES DE LA INTEGRAL
3. CÁLCULO DE VOLÚMENES DE SÓLIDOS DE REVOLUCIÓN
Cálculo de Volúmenes de Sólidos de Revolución.
En los ejemplos que desarrollaremos a continuación, utilizaremos el hecho básico de que un
rectángulo de base dx y altura f(x), como en la figura, al girar en torno al eje x, genera un
cilindro de radio f(x) y altura dx:
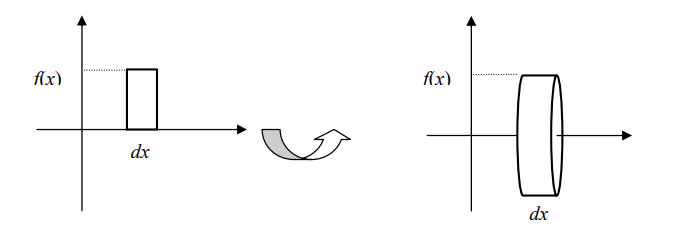
Cuyo volumen es
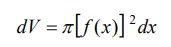
En los siguientes ejemplos los diferenciales de volumen serán de esta naturaleza.
Como en el caso del cálculo de áreas, el volumen del sólido lo obtendremos tomando límites de aproximaciones que también las identificaremos con integrales. En estos casos, las aproximaciones al volumen se harán por medio de volúmenes de cilindros, cada uno de los cuales está generado por la rotación de un rectángulo de los que aproximan el área de la región que lo genera.
A partir de aquí no utilizaremos explícitamente las subdivisiones, sino sólo los elementos
genéricos ( diferenciales de área y de volumen).
Ejemplo 1. Encuentre el volumen del sólido obtenido al girar en torno al eje x el triángulo
de la figura:
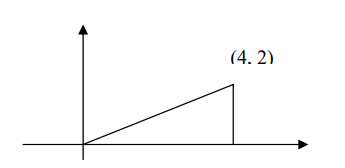
Solución: Al girar esta región alrededor del eje x, se genera un cono de altura 4 y radio 2
como se muestra en la siguiente figura.
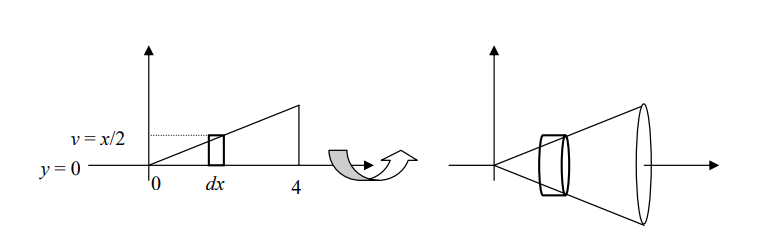
Aunque sólo se dibuja un rectángulo genérico, debemos pensar que los rectángulos son una aproximación al área de la región y que al girar el sistema completo (la región y los rectángulos que la aproximan) obtendremos una aproximación al volumen del sólido mediante los volúmenes de cilindros. El límite de dichas aproximaciones, la integral, nos dará el volumen del sólido generado.
Para cada x ∈ [0, 4], al girar el rectángulo genérico de la figura de la izquierda, en torno al
eje x, genera el cilindro genérico de la derecha, el cual tiene volumen:
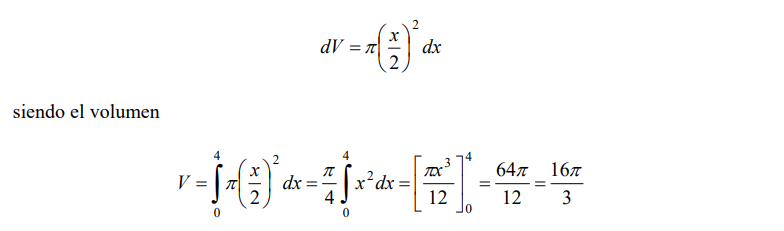
Lo cual verifica el resultado dado por la conocida fórmula de la geometría para el volumen
de un cono de altura h y radio r.
Ejemplo 2. Demuestre que el volumen de un cono de radio r y altura h es:
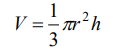
Solución: El cono de altura h y radio r será generado por la región de la figura, en la que la
ecuación de la recta que pasa por (0, 0) y (h, r) es
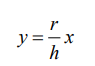
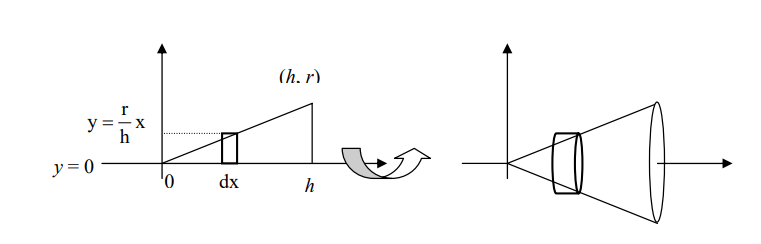
Para cada x ∈ [0, h], al girar el rectángulo genérico de la figura de la izquierda, en torno al
eje x, se obtiene el cilindro genérico de la derecha, cuyo volumen es:
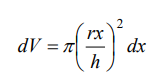
siendo el volumen total del sólido de revolución:
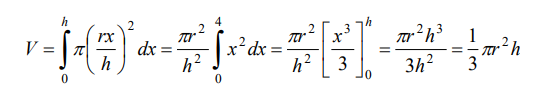
Utilizando este mismo método podemos encontrar volúmenes de otros sólidos de
revolución para los que la geometría no proporciona fórmulas, como el siguiente:
Ejemplo 3. Encuentre el volumen del sólido obtenido al girar en torno al eje x la parábola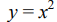 
en el intervalo [0, 1]
Solución:
Ejemplo 4. Encuentre el volumen de una esfera de radio 3.
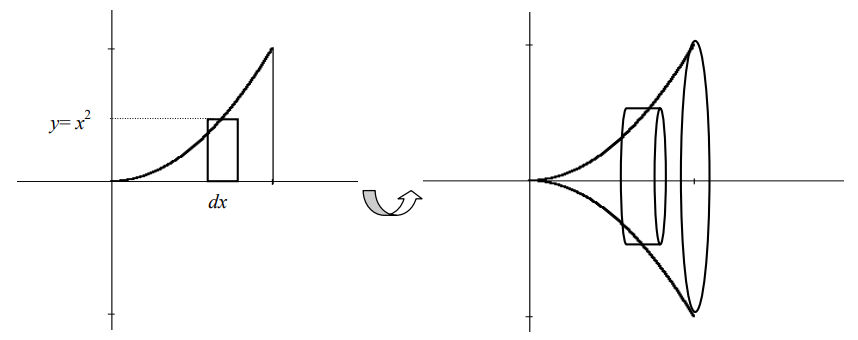
Solución:
Para cada x ∈ [-3, 3]
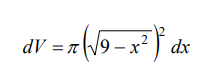
y el volumen de la esfera es
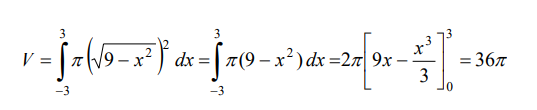
Lo cual verifica el resultado de aplicar la fórmula para calcular el volumen de una esfera de
radio r, que nos da la geometría. Con el procedimiento anterior, deduciremos esta fórmula
en el siguiente ejemplo.
Ejemplo 5. Demuestre que el volumen de una esfera de radio r es
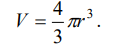
Solución: La ecuación de la circunferencia de radio r que generará a la esfera de radio r es:
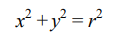
Tomando como referencia el dibujo anterior, sólo que considerando la función
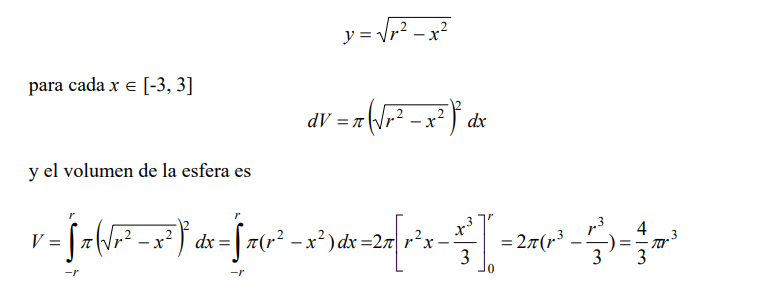
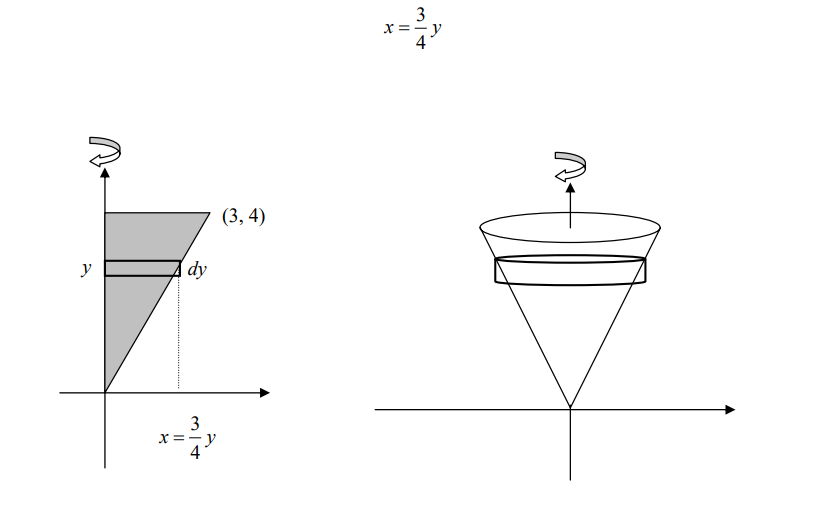
Ejemplo 6. Encuentre el volumen del sólido obtenido al girar en torno al eje y la región
delimitada por el eje y y la recta de la figura.
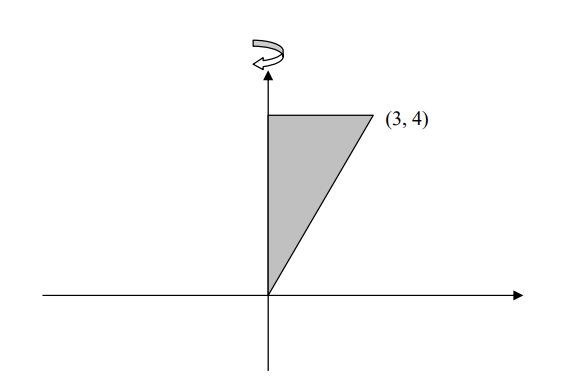
Solución: Al girar en torno al eje y, esta región generará un cono de radio 3 y altura 4.
Obsérvese que en este caso es conveniente utilizar diferenciales horizontales para que al
girarlos entorno al eje y generen cilindros como en el caso anterior. Para hacer esto
debemos tener la ecuación de la recta en términos de y.
