3.1 APLICACIONES DE LA INTEGRAL
5. PRESIÓN HIDROSTÁTICA
Presión Hidrostática.
En esta aplicación de la integral abordaremos el problema de determinar la presión con la que un líquido actúa sobre una pared vertical, o sobre una de las paredes del recipiente que lo contiene.
Los principios básicos se detallan a continuación
Presión sobre una superficie horizontal
El caso más sencillo sería el de determinar la presión con la que el agua actúa sobre el
fondo de un recipiente lleno de agua. En este caso y en general para una superficie plana
horizontal bajo el agua, una ley de la Hidrostática nos dice que la presión del agua sobre
ella es igual al peso de la columna de agua que soporta, es decir, de una columna de agua
que tiene esta superficie como base y cuya altura es la profundidad a la que se encuentra
sumergida dicha superficie. Como se trata de agua, cuyo peso específico es 1, el peso de
esta columna numéricamente es igual al volumen.
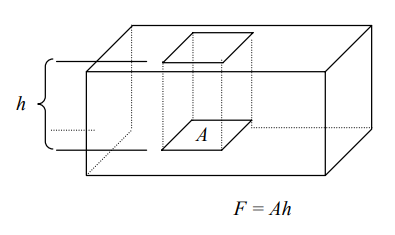
Presión sobre una superficie no horizontal.
Si la superficie sumergida no está horizontal, entonces los diversos puntos de ella se encuentran a diferentes profundidades y no podemos hablar de la profundidad de sumersión de la superficie como un todo. Pero, si esta superficie es muy pequeña, entonces es posible hacer cálculos aproximados, suponiendo que todos sus puntos están a una misma profundidad, la cual es considerada como la profundidad a la que se encuentra la superficie.
Trataremos pues con este tipo de superficies planas muy pequeñas y para determinar la
presión sobre ella, imaginemos que se hace girar la superficie alrededor de uno de sus
puntos, como si se tratara de una hoja de persiana, hasta que la superficie toma una
posición horizontal. Como la presión en un punto se transmite en todas direcciones con la
misma intensidad y sólo depende de la profundidad, y la superficie es muy pequeña, al
girar, todos sus puntos se mantienen aproximadamente a la misma profundidad, por lo que
la presión sobre ella no variará sensiblemente con la posición de giro y por lo tanto podemos considerar que la superficie se encuentra en posición horizontal y calcularle a esta
la presión.
Ejemplo 1. Determinar la Fuerza (Presión Hidrostática) con la que el agua actúa sobre la
pared frontal del siguiente recipiente lleno de agua de la figura.
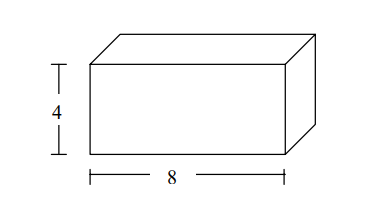
Solución: Ubiquemos la pared frontal en un sistema coordenado.
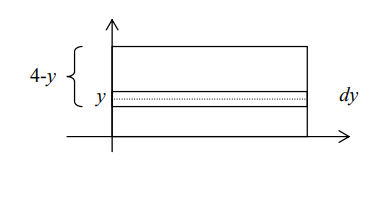
Para cada y ∈ [0, 4], consideremos el pequeño rectángulo de largo 8 y altura dy, el cual se
encuentra a una profundidad (4 - y). En base a la discusión anterior, la fuerza con la que el
agua actúa sobre ella será aproximadamente igual a la fuerza con que actuaría sobre el
mismo rectángulo pero en posición horizontal, es decir, el diferencial de Fuerza será:
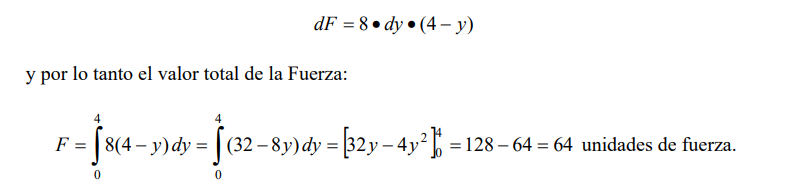
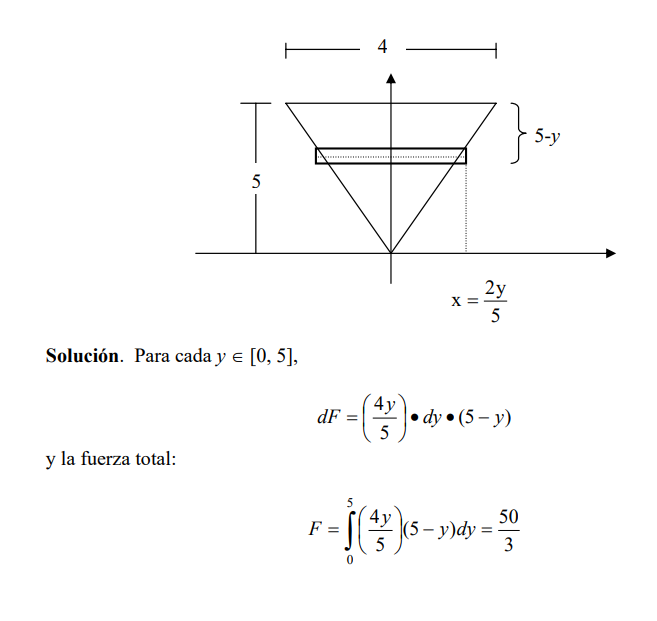
Ejemplo 2. Determinar la presión con la que el agua actúa sobre una placa triangular, como
la de la figura, sumergida verticalmente en agua.