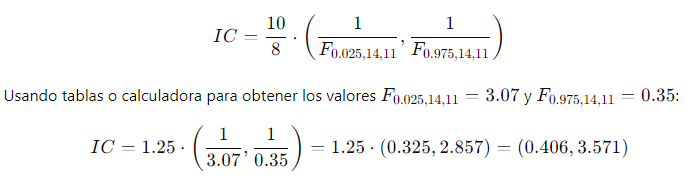Temas de guia para la unidad 1.- Estimación
| Site: | Moodle ITST |
| Course: | Métodos Estadisticos |
| Book: | Temas de guia para la unidad 1.- Estimación |
| Printed by: | Guest user |
| Date: | Monday, 28 April 2025, 7:53 PM |
Description
En esta pagina encontraras algunos ejemplos y ejercision de como implementar las formulas y aplicarlas.
Table of contents
- 1. 1.1 Tipos de Estimaciones y sus Características
- 2. 1.2 Teorema del Límite Central (TLC) Explicación del TLC
- 3. 1.3 Intervalos de Confianza para la Media
- 4. 1.4 Estimación de Proporciones para una Muestra Única
- 5. 1.5 Intervalo de Confianza para la Diferencia de Dos Proporciones
- 6. 1.6 Intervalos de Confianza para la Relación de Dos Varianzas
1.1 Tipos de Estimaciones y sus Características
Como sacar la desbiacion estandar (S) o alfa.
Tipos de Estimaciones
Estimación Puntual: Se refiere a un solo valor estimado basado en datos muestrales para representar un parámetro poblacional. Por ejemplo, la media muestral () como una estimación puntual de la media poblacional ().
Estimación por Intervalo: Se trata de un rango de valores dentro del cual se espera que se encuentre el parámetro poblacional con un cierto nivel de confianza. Por ejemplo, un intervalo de confianza para la media poblacional.
con la explicacion de que es los tipos de estimaciones y sus caracteristicas.
Informacion del significado de simbologias:
Fórmulas Comunes
- Media muestral ():
- : Número de observaciones en la muestra.
- : Observación individual en la muestra.
Ejercicio 1: Estimación Puntual de la Media
En una parcela de trigo, se seleccionan al azar 10 plantas y se mide su altura en centímetros: 85, 90, 88, 92, 89, 87, 91, 86, 93, 88. Calcula la media muestral.
Solución:
A continiacion te dejo un enlace:
en el cual podras ver el ejemplo de como sacar la media de una forma facil y sencilla tanto en excel como manualmente.
1.2 Teorema del Límite Central (TLC)
Explicación del TLC
El Teorema del Límite Central establece que, para un tamaño de muestra suficientemente grande, la distribución de la media muestral de una variable aleatoria será aproximadamente normal, independientemente de la distribución original de la población.
Te dejo un enlace a continuacion para que quede mas clara en que consiste el teorema del limite central.
Fórmula del Teorema del Límite Central

Donde:
- : Media poblacional.
- : Desviación estándar de la población.
- : Tamaño de la muestra.
Ejercicio 2: Aplicación del TLC
Supón que la altura de las plantas de maíz en un campo sigue una distribución desconocida con y . Si se toma una muestra de 25 plantas, ¿cuál es la distribución aproximada de la media muestral?
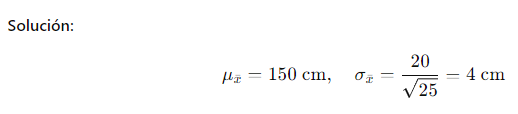
La media muestral seguirá una distribución normal aproximadamente con media 150 cm y desviación estándar 4 cm.
1.3 Intervalos de Confianza para la Media
1.3.1 Con Distribución Normal
Fórmula del Intervalo de Confianza para la Media con Distribución Normal
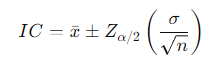
Donde:
- : Media muestral.
- : Valor crítico de la distribución normal estándar para un nivel de confianza .
- : Desviación estándar de la población.
- : Tamaño de la muestra.
Enlace de como utilizar la tabla de distibucion normal (Z alfa medios).
Enlace para entender mejor la aplicacion de los calculos de distribucion normal.
1.3.2 Con Distribución "t" de Student
Fórmula del Intervalo de Confianza para la Media con Distribución "t"
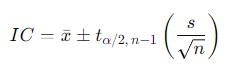
Donde:
- : Valor crítico de la distribución "t" de Student con grados de libertad.
s
ejemplo:
Ejercicio 3: Intervalo de Confianza con Distribución Normal
En una investigación sobre el rendimiento de las plantas de tomate, se encontró que la media muestral es de 2.5 kg/planta con una desviación estándar poblacional conocida de 0.5 kg. Si se selecciona una muestra de 36 plantas, calcula el intervalo de confianza al 95%.
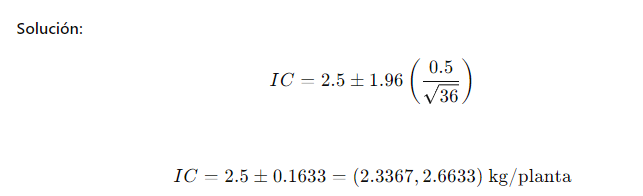
1.3.1 Determinación del Tamaño de Muestra con Grado de Confianza y Estimación de μ
Fórmula para el Tamaño de Muestra
Donde:
- : Margen de error permitido.
Ejercicio 4: Determinación del Tamaño de Muestra
Para estimar la altura media de las plantas de soya con un margen de error de 1 cm y un nivel de confianza del 95%, y con una desviación estándar conocida de 4 cm, determina el tamaño mínimo de la muestra.
Solución:
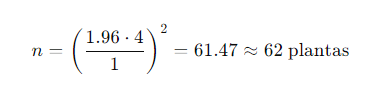
1.4 Estimación de Proporciones para una Muestra Única
Fórmula del Intervalo de Confianza para una Proporción
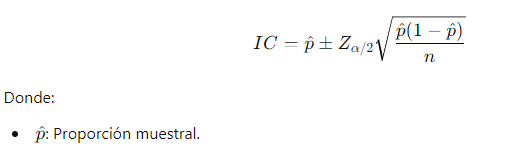
Ejercicio 5: Estimación de una Proporción
En una muestra de 200 plantas de maíz, 160 fueron resistentes a una plaga. Calcula el intervalo de confianza al 95% para la proporción de plantas resistentes.
Solución: NOTA: recuerda que P=n/N donde es la muestra tomada de (N), y (N) es el total global de la muestra.
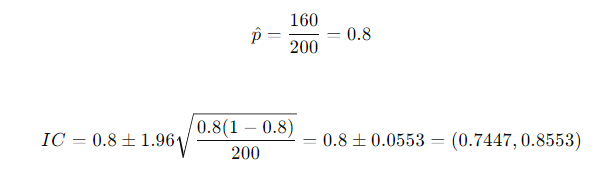
1.5 Intervalo de Confianza para la Diferencia de Dos Proporciones
Fórmula del Intervalo de Confianza para la Diferencia de Proporciones
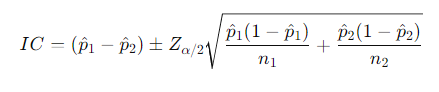
Donde:
- y : Proporciones muestrales de dos grupos diferentes.
- y : Tamaños de las muestras de los dos grupos.
Ejercicio 6: Comparación de Proporciones
En dos campos diferentes, 150 de 200 plantas y 120 de 180 plantas fueron resistentes a una enfermedad. Calcula el intervalo de confianza al 95% para la diferencia en las proporciones.
Solución:
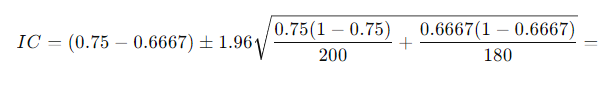
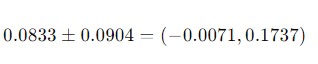
1.6 Intervalos de Confianza para la Relación de Dos Varianzas
Fórmula del Intervalo de Confianza para la Relación de Varianzas
Utilizacion de las tablas de F:
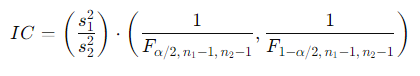
Donde:
- y : Varianzas muestrales de los dos grupos.
- : Valor crítico de la distribución F.
Ejercicio 7: Intervalo de Confianza para la Relación de Varianzas
En un experimento, se midieron dos varianzas de rendimiento en parcelas agrícolas: y con tamaños de muestra de 15 y 12, respectivamente. Calcula el intervalo de confianza al 95% para la relación de varianzas.
Solución: Primero, se buscan los valores críticos de la distribución F con 14 y 11 grados de libertad.