1.2 Definiciones básicas: variable (dependiente e independiente), relación, función, dominio y rango. Tipos de funciones
| Sitio: | Moodle ITST |
| Curso: | Cálculo Diferencial |
| Libro: | 1.2 Definiciones básicas: variable (dependiente e independiente), relación, función, dominio y rango. Tipos de funciones |
| Impreso por: | Invitado |
| Fecha: | lunes, 28 de abril de 2025, 18:02 |
1. Definiciones básicas y tipos de funciones
¿QUÉ ES UNA FUNCIÓN?
Una función es una regla de correspondencia entre dos conjuntos de tal manera que a cada elemento del primer conjunto le corresponde uno y sólo un elemento del segundo conjunto.
¿QUÉ ES EL DOMINIO Y RANGO DE UNA FUNCIÓN?
El dominio de una función es el conjunto de todos los valores de la variable independiente (representada por la variable ) que pueden ser usados en la función. El rango de una función es el conjunto de todos los valores de la variable dependiente (representada por la variable ) que resultan de los valores del dominio.
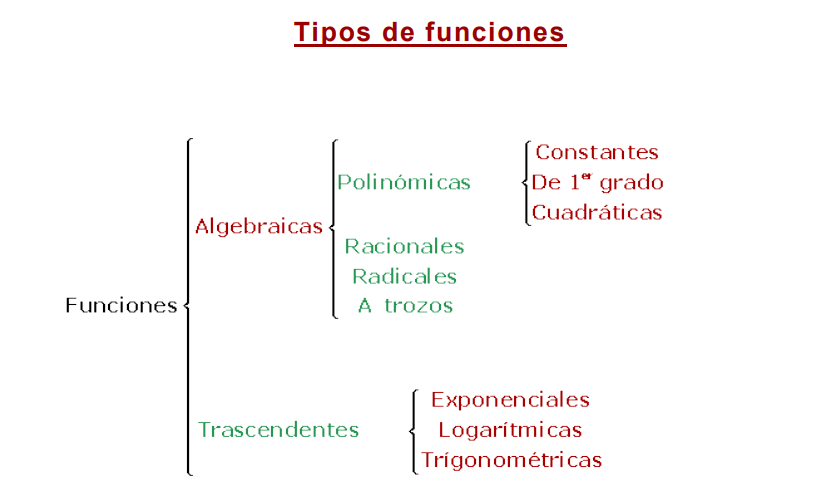
Clasificación de funciones
Funciones algebraicasEn las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.
Las funciones algebraicas pueden ser:
Funciones explícitas Si se pueden obtener las imágenes de x por simple sustitución. f(x) = 5x - 2
Funciones implícitas Si no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.
5x - y - 2 = 0
Funciones polinómicas
Son las funciones que vienen definidas por un polinomio.
f(x) = a0 + a1 x + a1 x² + a1 x³ +··· + an x n
Su dominio es , es decir, cualquier número real tiene imagen.
Funciones constantes
El criterio viene dado por un número real.
f(x)= k
La gráfica es una recta horizontal paralela a al eje de abscisas.
Funciones polinómica de primer grado
f(x) = mx +n
Su gráfica es una recta oblicua, que queda definida por dos puntos de la función. Funciones cuadráticas
f(x) = ax² + bx +c
Son funciones polinómicas de segundo grado, siendo su gráfica una parábola. Funciones racionales
El criterio viene dado por un cociente entre polinomio:
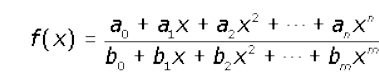
El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.
Funciones radicales
El criterio viene dado por la variable x bajo el signo radical.
El dominio de una función irracional de índice impar es R.
El dominio de una función irracional de índice par está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.
Funciones trascendentes
La variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.
Función exponencial
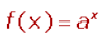
Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia a x se llama función exponencial de base a y exponente x. Funciones logarítmicas
La función logarítmica en base a es la función inversa de la exponencial en base a.
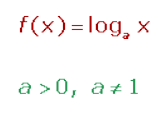
Funciones trigonómetricas
Función seno
f(x) = sen x
Función coseno
f(x) = cosen x
Función tangente
f(x) = tg x
Función cosecante
f(x) = cosec x
Función secante
f(x) = sec x
Función cotangente
f(x) = cotg x