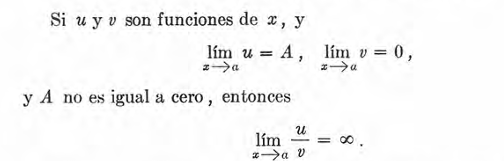2.1 Conceptos, teoremas y propiedades de los limtes
| Sitio: | Moodle ITST |
| Curso: | Cálculo Diferencial |
| Libro: | 2.1 Conceptos, teoremas y propiedades de los limtes |
| Impreso por: | Invitado |
| Fecha: | lunes, 28 de abril de 2025, 18:00 |
Descripción
Descripción: Conceptos, teoremas y propiedades de los limtes
1. Conceptos, teoremas y propiedades de los limtes
Límite de una variable.
La noción de una variable que se
aproxima a un limite se encuentra, en la Geometría elemental, al
establecer o deducir la fórmula que da el área del círculo. Se considera
el área de un polígono regular inscrito con un número n cualquiera de
lados, y se supone, después, que n crece infinitamente. El área
variable tiende así hacía un limite, y este límite se define como área
del círculo . En este caso, la variable v (área) aumenta indefinida
mente, y la diferencia a - v (siendo a el área del círculo) va disminu
yendo hasta que, finalmente, llega a ser menor que cualquier número
positivo escogido de antemano, sin importar lo pequeño que éste se
haya elegido.DEFINICIÓN DE LIMITE
Se dice que la variable v tiende a la constante l como límite, cuando los valores sucesivos de v son tales que el valor numé rico de la diferencia v - l puede llegar a ser, finalmente, menor que cualquier número positivo predeterminado tan pequeño como se quiera.La relación así definida se escribe lim v = l. Por conveniencia, nos serviremos de la notación v -7 l, que se leerá "v tiende hacia el límite l" o, más brevemente, "v tiende al". (Algunos autores usan la notación v -:"l . )

Límite de una función.
En las aplicaciones de la definición de límite, se presentan usualmente casos como el siguiente: se tiene una variable v y una función dada z de v, y se supone que la variable v recibe valores tales que v -7 l. Tenemos que examinar entonces los valores de la variable dependiente z e investigar, particularmente, si z tiende también a un limite. Si efectivamente existe una constante a tal que lím z = a, entonces se expresa est.a relación escribiendo: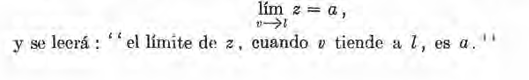
Teoremas sobre límites.
En el cálculo del límite de una fun ción tienen aplicación los teoremas siguientes. Las demostraciones se darán en el Artículo 20 . Supongamos que u, v y w sean funciones de una variable x y que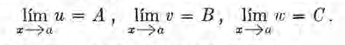
Entonces son ciertas las siguientes relaciones.
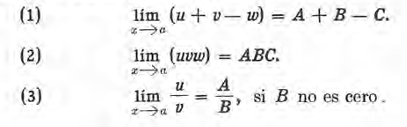
En breves palabras: el límite de una suma algebraica, de un producto o de un cociente es igual, respectivamente, a la suma algebraica, al pro ducto o al cociente de los límites respectivos, con tal de que, en el último caso, el límite del divisor no sea cero.
Si c es una constante (independiente de x) y B no es cero, de lo anterior se deduce:
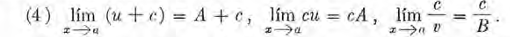

Funciones continuas y discontinuas.
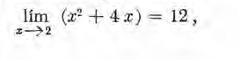
Observamos que la solución es el valor de la función para x = 2 ; es decir, el valor límite de la función cuando x tiende a 2 es igual al valor de la función para x = 2. En este caso decimcs que la función es continua para x = 2. La definición general es la siguiente:
DEFINICIÓN. Se dice que una función f(x) es continua para x= a
si el límite de la función, cuando x tiende a a, es igual al valor de
la función para x = a. En símbolos, si
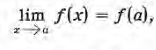
entonces f (x) es continua para x = a. Se dice que la función es discontinua para x = a si no se satisface esta condición.
Llamamos la atención de los dos casos siguientes:
CASO l. Como ejemplo sencillo de una función que es continua para un valor particular de la variable, consideremos la función:

CASO II. La definición de función continua supone que la función está definida para x = a . Sin embargo, si este no es el caso, a veces es posible asignar a la función tal valor para x = a que la condición de continuidad se satisfaga. En estos casos se aplica el siguiente teorema:

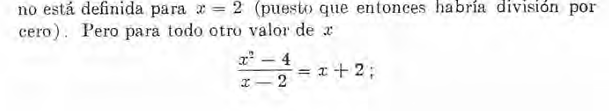
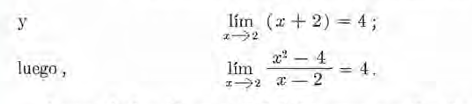
Aunque la función no está definida para x = 2, si arbitrariamente asignamos a ella para x = 2 el valor 4, se hace continua para este valor. Se dice que una función f (x) es cont1'nua en un intervalo cuando es continua para todos los valores de x dentro de este intervalo.
Infinito (∞)
Si el valor numérico de una variable v llega a ser y permanece mayor que cualquier número positivo asignado de antemano, por grande que éste sea, decimos qlle v se vuelve infinita . Si v toma solamente valores positivos, se hace infinita positivamente; si solamente toma valores negativos, se hace infinita negativamente. La notación que se emplea para los tres casos es
Ciertos límites particulares que se presentan frecuentemente se dan a continuación. La constante c no es cero.



Estos límites particulares son útiles para hallar el límite del cociente de dos polinomios cuando la variable se hace infinita . El siguiente ejemplo ilustrará el método .

El límite de cada término que contiene a x, tanto en el numerador como en el denominador del segundo miembro. es cero. Por consiguiente se obtiene la solución. En cualquier caso análogo se procede como sigue: Se diuiden numerador y denominador por la mayor potencia de la variable que entre en la fracción.