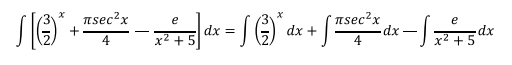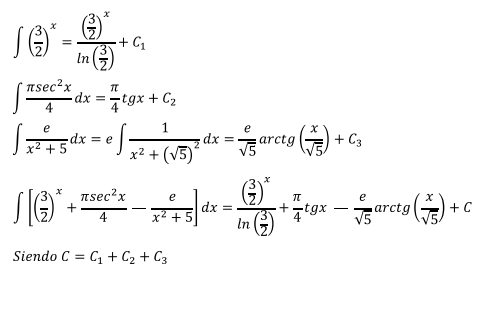2.1 MÉTODOS DE INTEGRACIÓN E INTEGRAL INDEFINIDA

               DEFINICIÓN DE INTEGRAL INDEFINIDA

Integrar es el proceso recíproco del derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x).

Se dice, entonces, que F(x) es una primitiva o antiderivada de f(x); dicho de otro modo las primitivas de f(x) son las funciones derivables F(x) tales que:

F'(x) = f(x).

Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en una constante.

[F(x) + C]' = F'(x) + 0 = F'(x) = f(x)

               Integración de formas elementales

Como ya se dijo, integrar es el proceso contrario a derivar. En la tabla 1 que se muestra a continuación, hay algunas fórmulas que sirven para integrar directamente.

Ejercicio 1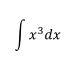    

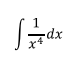
Solución: En este caso, aplicamos la fórmula 2 de la Tabla 1 haciendo n=3

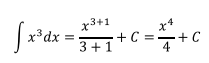
Comprobación: Derivando el resultado se debe regresar a la integral original

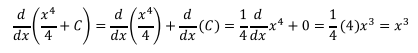
Ejercicio 2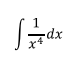 

Solución: Aplicamos la misma fórmula del ejercicio anterior, esta vez haciendo n= -4

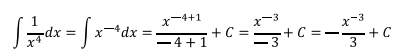
Comprobación

Ejercicio 3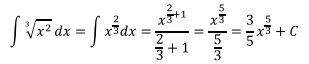  

Comprobación: Se la deja al estudiante

Ejercicio 4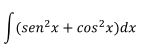 

Aplicando la identidad trigonométrica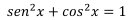  

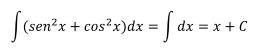
Comprobación: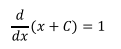    

Aplicando la identidad trigonométrica mencionada se llega a la integral original

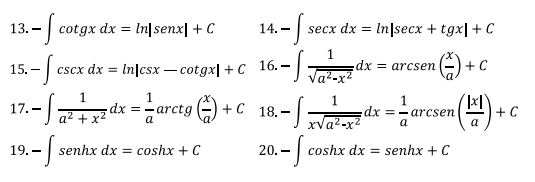
Existen dos propiedades muy usadas en la solución de ejercicios de cálculo integral que son:

Propiedad 1.1 El integral de las suma o resta de dos más funciones es igual a la suma o resta de la integral de cada una de esas funciones.

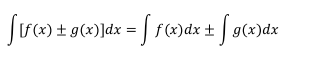
Propiedad 1.2 El integral de la multiplicación de una constante por una función es igual a la multiplicación de dicha constante por el integral de la función.

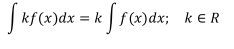
Ejercicio 1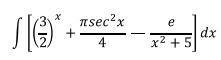  

Aplicando la propiedad 1.1 la integral anterior podemos descomponerla en tres integrales más sencillas