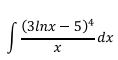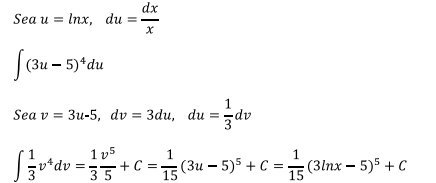2.1 MÉTODOS DE INTEGRACIÓN E INTEGRAL INDEFINIDA
2. 2.2 TÉCNICAS DE INTEGRACIÓN: CAMBIO DE VARIABLE
TÉCNICAS DE INTEGRACIÓN
En la mayor parte de los casos, las funciones no se las puede integrar usando directamente las fórmulas de la Tabla 1. Para estos casos existen técnicas que nos permiten hacer manipulaciones hasta llegar a la aplicación directa de la fórmula. Estas técnicas se las presenta a continuación.
Cambio de variable
En muchas ocasiones, la integración de una función puede ser
tremendamente larga, sin embargo un adecuado reemplazo de la variable original por otra, puede simplificar enormemente el trabajo,
por ejemplo:
Ejercicio 1 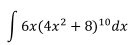
Si se quiere resolver esta integral aplicando alguna o algunas de
las fórmulas de la Tabla 1, habría que resolver el paréntesis multiplicando 10 veces el mismo integral para luego multiplicar ese resultado por
6x. Este es un procedimiento muy largo, lo recomendable es hacer una
sustitución. En este caso la sustitución recomendada es hacer
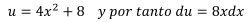
Despejando dx,
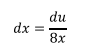
Y reemplazando en la integral original se tiene:
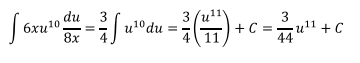
Reemplazando u para regresar a la variable original, se tiene que
el resultado de la integral es:
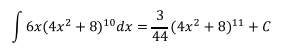
El estudiante puede comprobar este resultado como ya se ha sugerido anteriormente.
Como se puede apreciar, con un apropiado cambio de variable,
el proceso de integración puede simplificarse mucho. Veamos estos
otros ejercicios.
Ejercicio 2 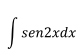
En este caso, ya que la fórmula dice senx, habrá que buscar una
sustitución apropiada para usar la fórmula (6). La sustitución más conveniente entonces es u=2x.
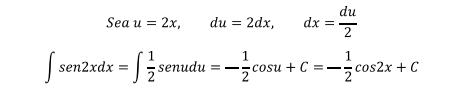
Se recomienda al estudiante realizar el ejercicio con sen3x, sen4x,
cos2x, cos3x y sacar sus conclusiones.
Ejercicio 3 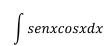
Con un poco de práctica, el estudiante puede llegar a reconocer
casos como éste en donde una función tiene como derivada la otra función, entonces la sustitución recomendada es
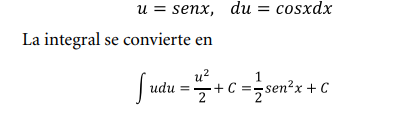
Ejercicio 4 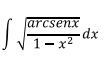
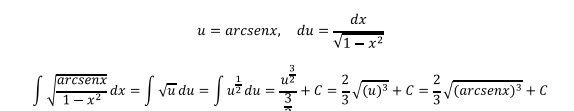
En ocasiones puede ser necesario más de un cambio de variable
como se aprecia en el siguiente ejercicio:
Ejercicio 5