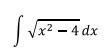2.1 MÉTODOS DE INTEGRACIÓN E INTEGRAL INDEFINIDA
5. 2.5 TÉCNICAS DE INTEGRACIÓN: POR SUSTITUCIÓN TRIGONOMÉTRICA
Integración por sustitución trigonométrica
Las funciones que tienen radicales generalmente son complicadas
de integrar, así es que conviene librarse de ellos. Una forma de lograrlo
es haciendo las sustituciones que se recomiendan a continuación:
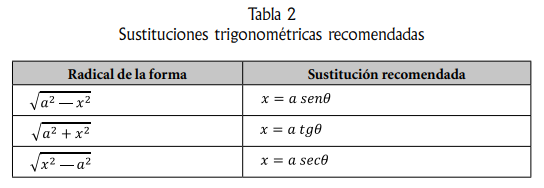
Ejercicio 1 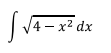
De acuerdo a la sustitución recomendada en la tabla 1, la sustitución que aplica en este caso es:
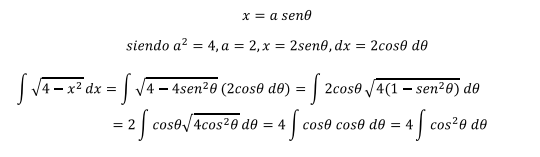
Este es un caso de integral trigonométrica en donde se usa la
identidad trigonométrica
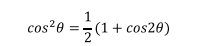
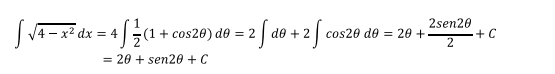
Es conveniente por una razón que se la explicará más adelante,
que la respuesta quede en función de ángulo simple y no de ángulos
múltiples como en este caso. Esto se lo puede hacer con la ayuda de la
siguiente identidad trigonométrica:
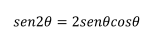
La respuesta quedaría entonces:
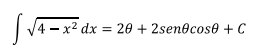
Para regresar a la variable original x se usa la sustitución original
que se hizo
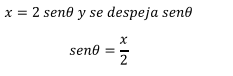
Por definición de la función trigonométrica seno, x es el lado
opuesto y 2 la hipotenusa. Con este dato se construye un triángulo rectángulo, de donde se sacan los datos que se necesitan para reemplazar
por la variable original x.
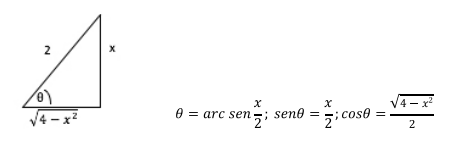
Reemplazando en la respuesta se tiene
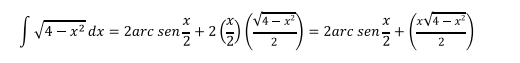
Ejercicio 2 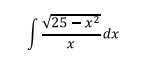

Para volver a la variable original, se procede tal como se explicó
en el ejercicio anterior

Con este dato se construye el triángulo rectángulo
Los datos que se sacan del triángulo para reemplazar en la respuesta son:
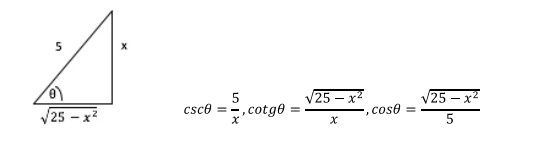
Reemplazando se tiene:
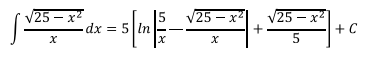
Ejercicio 3 
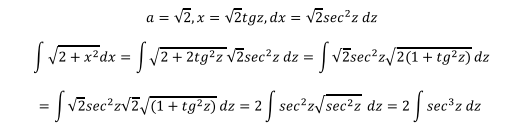
Este caso no está contemplado en ninguno de los casos de integrales trigonométricas antes expuesto. La solución se la realizará por el
método de integración por partes (Villena, s.f.).
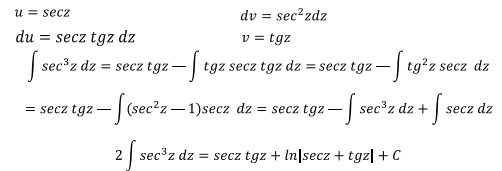
El estudiante debe notar que en la expresión anterior, ya está incluido el 2 de la respuesta anterior de tal manera que
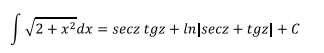
Regresando a la variable original,

Ejercicio 4 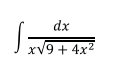
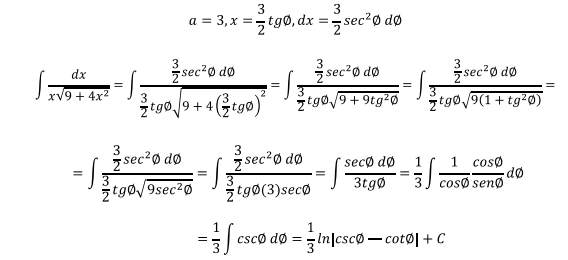
Para regresar a la variable x se construye el triángulo rectángulo a
partir de la sustitución original hecha:
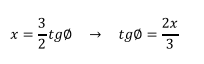
Extrayendo del triángulo los datos necesarios para reemplazar en
la respuesta se tiene:
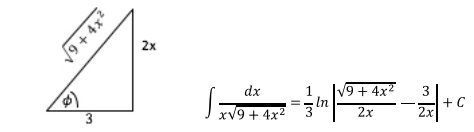
Ejercicio 5