3.1 APLICACIONES DE LA INTEGRAL

Cálculo de Áreas

En los siguientes ejemplos encontraremos el área de una región dada. Dicha región será considerada como el área comprendida entre dos curvas, cuyas intersecciones definen el intervalo que subdividiremos en n partes iguales, a partir de lo cual encontraremos aproximaciones cuyo límite será el área buscada. A este límite lo identificaremos como una integral.

Posteriormente resumiremos este proceso de integración con la introducción de diferenciales de áreas y no trataremos explícitamente con las subdivisiones del intervalo de integración.

Ejemplo 1. 

Encuentre el área de la región delimitada por la parábola 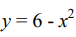    y la recta    y = x

Solución:

Primeramente encontraremos los puntos de intersección, igualando la  parábola 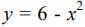  y la recta y = x, para determinar el intervalo de integración.

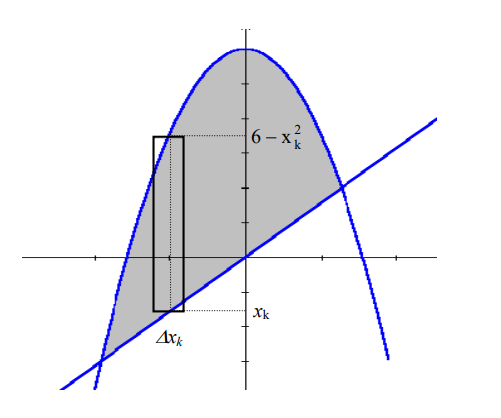
El área del rectángulo genérico de base 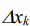  (el área del k-ésimo rectángulo determinado por la partición) es:

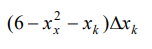
Nótese que, para encontrar la altura del rectángulo debemos saber cuál es la curva que queda por arriba y cuál la que queda por abajo. 

Un valor aproximado al área buscada es la suma de los rectángulos determinados por la subdivisión:

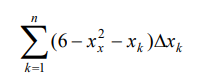
y el valor exacto del área es el límite de estas aproximaciones, el cual lo identificamos con una integral:

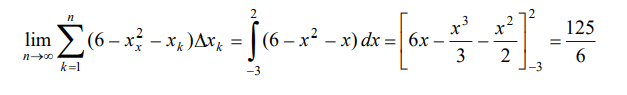
En base a esto, directamente escribimos el área del rectángulo genérico, al que llamaremos dA, como:

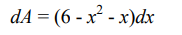
encontrando el área buscada como proceso de integrar esta expresión

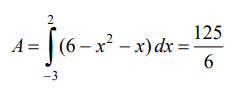
Ejemplo 2.

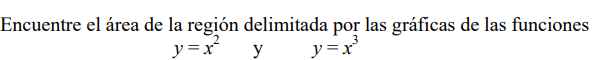
Solución:

Valor exacto del área:

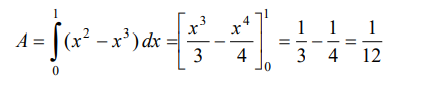
Ejemplo 3.

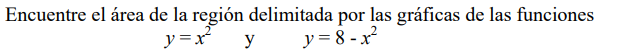
Solución:

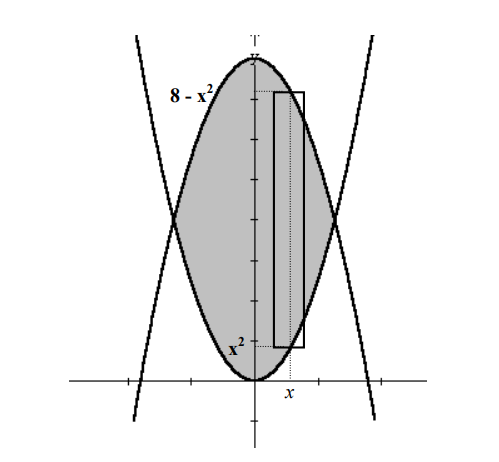
Los puntos de intersección de las curvas satisfacen

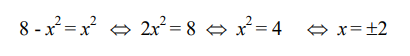
El diferencial de área es.

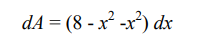
y el valor del área:

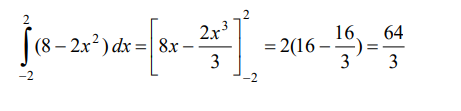
Ejemplo 4.

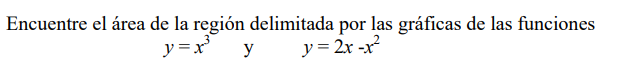
Solución:

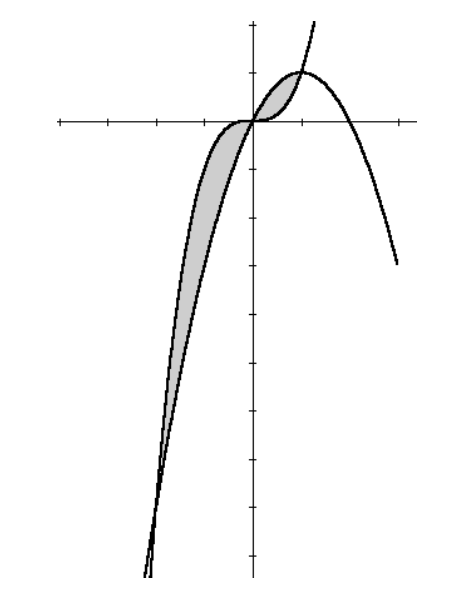
Las intersecciones entre estas dos curvas están dadas por las soluciones de la ecuación:

Así pues tendremos que encontrar los diferenciales de área correspondientes a cada uno de estos intervalos y efectuar integraciones por separado.

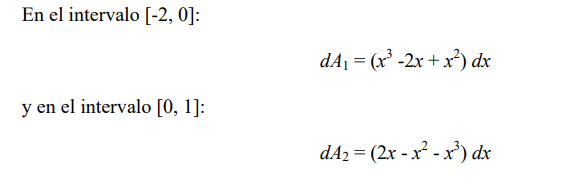
por lo que el área será:

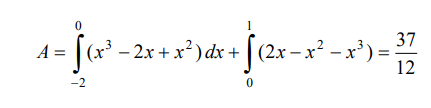
Ejemplo 5. 

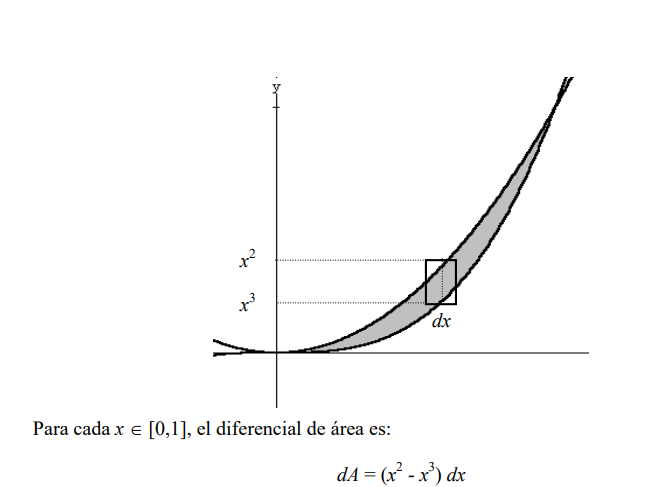
Encuentre el área de la región delimitada por las gráficas de la parábola 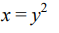y la recta x - 2y -3 =0

Solución:

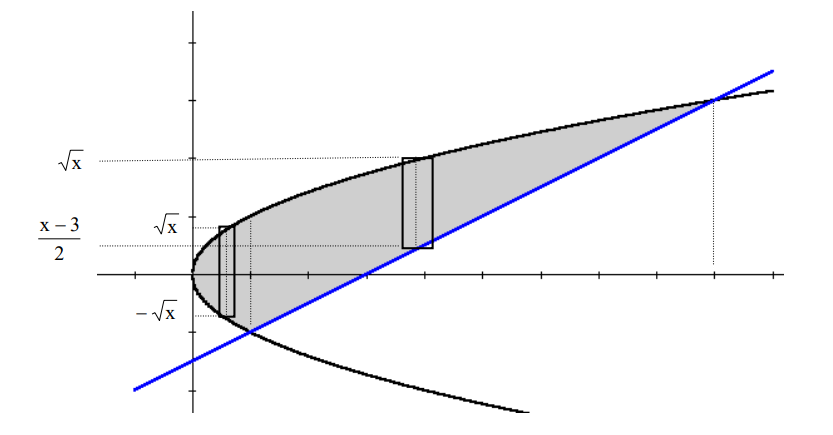
Las ordenadas de las intersecciones están dadas por las soluciones de:

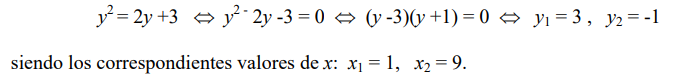
Si procedemos como en el ejemplo anterior, tendríamos que calcular el diferencial de área correspondiente al intervalo [0, 1] y el correspondiente al intervalo [1, 9], siendo éstos:

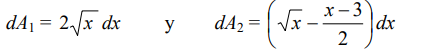
el valor del área:

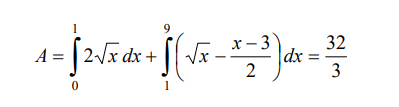
El problema que nos condujo a tener que separar en dos integrales se debe a que en toda el área de integración no podemos encontrar un rectángulo genérico uniforme, es decir, uno cuyo extremo superior se encuentre en la función de arriba y el extremo inferior en la de abajo. 

Si en vez de considerar diferenciales de área verticales, los tomamos horizontales, sí será posible encontrar un rectángulo genérico uniforme, solo que tendremos que expresar a nuestras funciones en términos de y, es decir, tendremos que trabajar con las funciones inversas correspondientes.

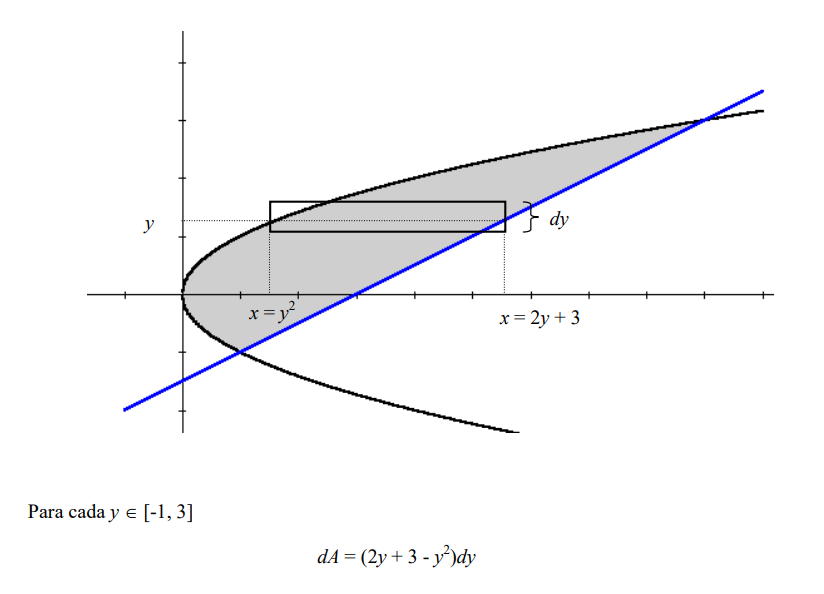
y por lo tanto el área es:

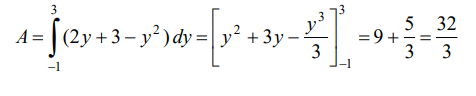
Ejemplo 6. 

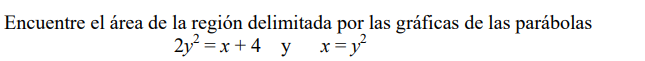
Solución

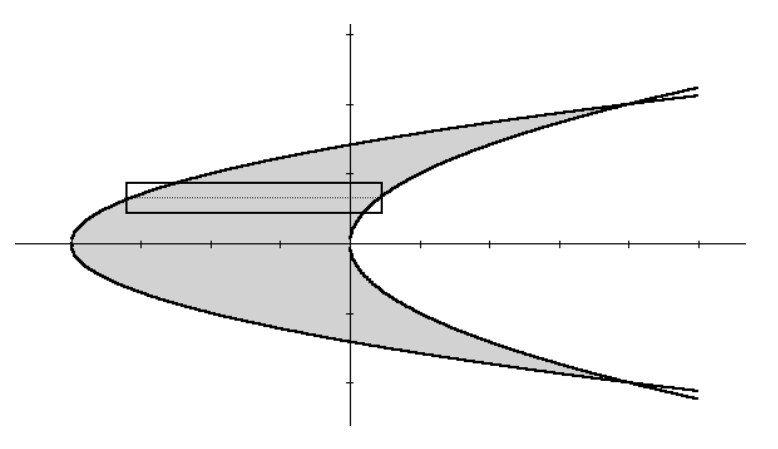
Como en el ejemplo anterior es más fácil utilizar diferenciales de área horizontales ya que no es posible encontrar un rectángulo vertical genérico.

Las intersecciones de estas parábolas satisfacen:

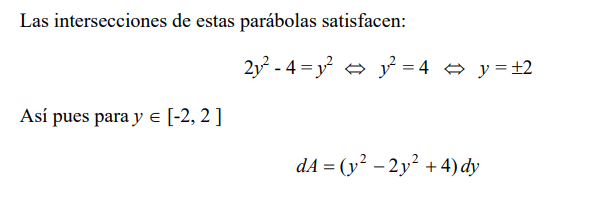
y el valor del área:

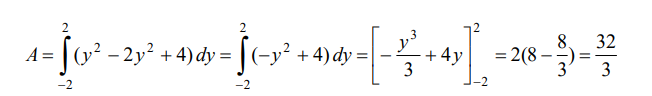
Observe que por la simetría de la región, podemos calcular el área encima del eje x, integrando de 0 a 1 y multiplicarla por dos, es decir