3.1 APLICACIONES DE LA INTEGRAL

Trabajo Mecánico.

En esta sección abordaremos problemas de la física cuya solución se obtiene por medio del mismo método de subdivisión, aproximaciones y límite de éstas para resolver finalmente por medio de integrales. 

En los problemas que veremos en esta sección, se requiere calcular el trabajo necesario para vaciar un cierto volumen de agua, la cual se extrae mediante una bomba. 

El principio básico que se aplicará en estos problemas, es el hecho de que el trabajo realizado al mover una partícula de materia esta dado por el producto entre la fuerza que actúa sobre dicha partícula (que deberá ser igual al propio peso) y la distancia que esta recorre. En el problema que nos ocupa, observe que para bombear del depósito una partícula del líquido, sólo es necesario levantarla hasta el borde ya que desde ese punto la partícula cae libremente por su propio peso. Así pues el problema se reduce a calcular el trabajo requerido para levantar sucesivamente todas las partículas del líquido hasta el borde del recipiente. 

Cuando cada partícula se levanta hasta el borde, recorre una distancia igual a su profundidad h, en el recipiente. La fuerza F necesaria para levantar una partícula es igual al producto del volumen V de la partícula, la densidad, ρ del líquido en cuestión y la fuerza de gravedad g; este producto manejado en las unidades correspondientes nos determina el peso de la partícula, por lo que el trabajo a realizar en el desplazamiento de la partícula hasta el borde del recipiente, está dado por

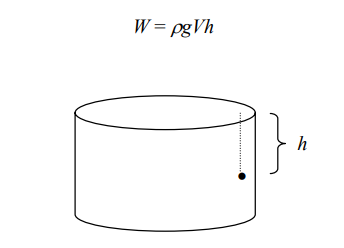
Para calcular el trabajo de vaciar el total de agua, haremos una subdivisión del volumen total en pequeños volúmenes de agua, calcularemos el trabajo para llevar hasta el borde cada una de ellos, sumaremos estos trabajos obteniendo una aproximación y posteriormente, el límite de las aproximaciones (de nuevo la integral) nos dará el trabajo buscado. 

Es conveniente aclarar que la suma de esos trabajos es una aproximación puesto que cada volumen de agua contiene partículas a distinta profundidad pero como consideraremos volúmenes muy pequeños, podemos suponer que todas las partículas se encuentran aproximadamente a la misma profundidad. 

En la siguiente figura el volumen V de agua se encuentra aproximadamente a una profundidad h

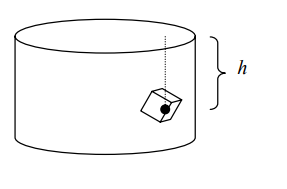
Por lo que el trabajo W para llevarlo al borde será:

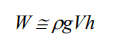
En realidad la subdivisión no la haremos en cubitos como los de la figura anterior sino en cilindros de altura muy pequeña como se verá en el siguiente ejemplo. 

Ejemplo 1. Encuentre el trabajo que se requiere para vaciar un depósito cilíndrico lleno de agua de 3m. de radio y 8m de altura. 

Solución: Ubiquemos nuestro depósito cilíndrico en un sistema de coordenadas con origen en el centro de la base y el eje y sobre la altura del mismo. Dividamos el volumen de agua del cilindro en n cilindros de radio 3 y altura 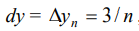  el cilindro genérico muestra en la figura.

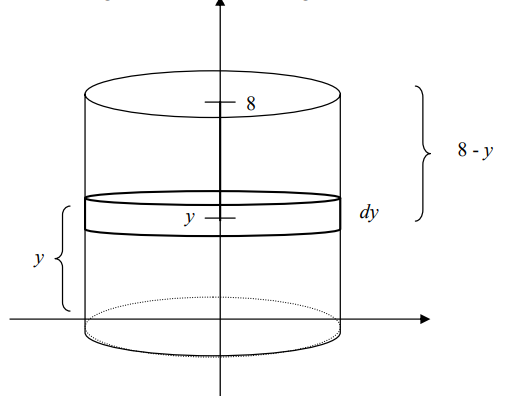
Para cada y ∈ [0, 8], calculamos el trabajo requerido para llevar hasta el borde el volumen del cilindro de radio 3 y altura dy (diferencial de trabajo dW)

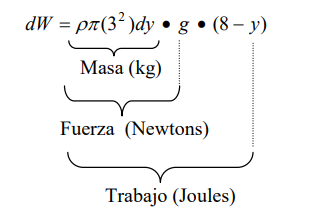
Por lo tanto el trabajo lo obtenemos integrando este diferencial:

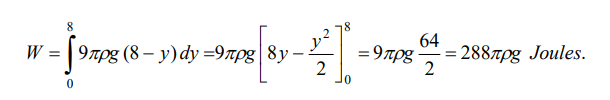
Ejemplo 2. Encuentre el trabajo que se requiere para vaciar un depósito cilíndrico de 3m. De radio y 8m de altura si se encuentra a la mitad de su capacidad. 

Solución: Se trata del depósito del problema anterior sólo que el nivel del agua se encuentra a 4 m de la base.

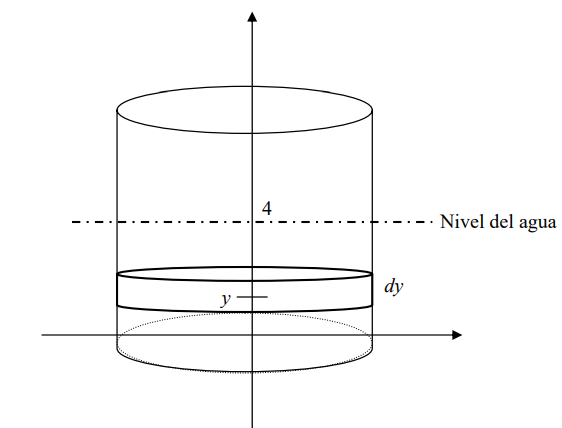
El diferencial de trabajo será el mismo que en el problema anterior y sólo cambiará el intervalo de integración a [0, 4], ya que consideraremos las rebanadas cilíndricas hasta la altura 4. 

Para cada y ∈ [0, 4]

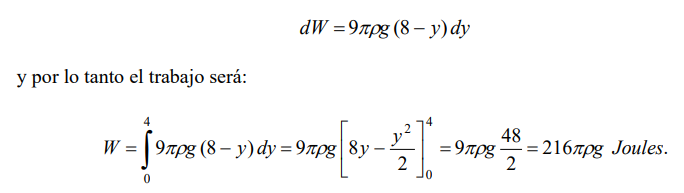
Observación: Nótese que aunque el volumen de agua es la mitad del ejemplo anterior, el trabajo para vaciarlo no difiere gran cosa del trabajo realizado cuando está lleno; esto se debe a que las partículas desde la base hasta la mitad de la altura están a una mayor profundidad que las de la otra mitad y por lo tanto "cuesta más trabajo" sacarlas. 

es decir, el diferencial de trabajo será el mismo que en el problema anterior y sólo cambiará el intervalo de integración a [0, 4]. 

Ejemplo 3. Encuentre el trabajo que se requiere para vaciar un depósito cónico lleno de agua, de 2m de radio y 5m de altura.

Solución:

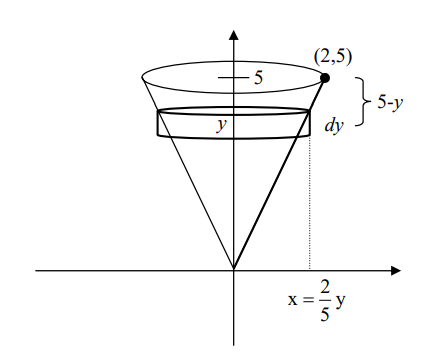
De nuevo ubicamos el depósito cilíndrico con su vértice en el origen, encontramos la ecuación de la recta que pasa por el origen y por el punto (2,5) (perfil del cono)

Ejemplo 4. Encuentre el trabajo que se requiere para vaciar un depósito cónico lleno de agua, de 2m de radio y 5m de altura, si se encuentra a la mitad de su capacidad. 

Solución:

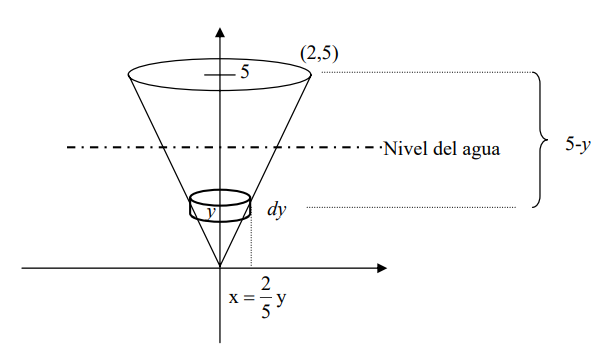
Como en el caso anterior tendremos que integrar el mismo diferencial, sólo que el intervalo de integración será desde 0 hasta la altura correspondiente a la mitad de la capacidad del cono. 

Tenemos pues que encontrar el valor de h para el cual el cono correspondiente tiene volumen igual a 10π / 3 , que es la mitad del volumen del depósito.

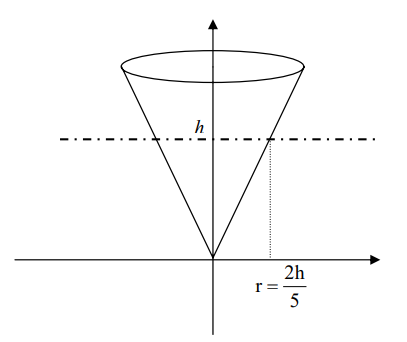
Es decir, tenemos que encontrar el valor de h para el cual

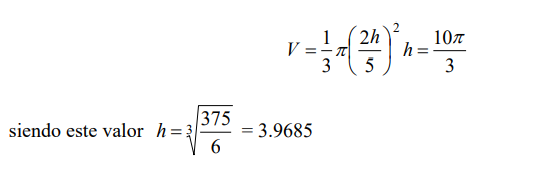
Así pues, el trabajo buscado es:

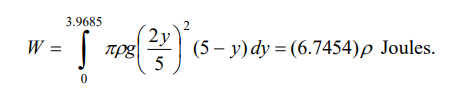
Ejemplo 5. Encuentre el trabajo que se requiere para bombear el agua de un tanque semiesférico lleno de agua, si el radio mide 3 m. 

Solución:

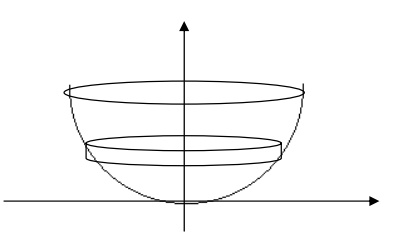
Si ubicamos el depósito como en la figura, la ecuación de la circunferencia de radio 3 y centro en el punto (0, 3) (perfil del depósito) es:

la cual puede integrarse fácilmente mediante el cambio de variable