Tema 1. Números reales
Axiomas de los números reales
Axiomas de los números reales
A continuación explicaremos las propiedades de los números reales para la suma o adición y para la multiplicación
A. Axiomas para la suma:
Las propiedades para la adición o suma son las siguientes:
1. Propiedad conmutativa
Esta propiedad nos indica que el orden de los sumandos no altera el valor de la suma, por ejemplo:
\( a + b = b + a \)
\( 6 + 3 = 3 + 6 \)
2. Propiedad asociativa de la suma
El corden como se agrupen los números para sumarlos, no altera el valor de la suma, por ejemplo:
\( (a + b) + c = a + (b + c) = (a + c) + b \)
\( (3 + 4) + 6 = 3 + (4 + 6) = (3 + 6) + 4 \)
3. Propiedad del elemento Neutro aditivo
Cualquier número real sumado con cero es igual al número real, por ejemplo:
\( a + 0 = a \)
\( 7 + 0 = 7 \)
4. Propiedad del elemento Neutro aditivo
Para cada número real, existe un número llamado inverso aditivo, que al sumarlo con el real, el resultado es cero, por ejemplo:
\( a + (-a) = 0 \)
\( 5 + (-5) = 0 \)
Propiedades para la Multiplicación
1. Propiedad conmutativa
El orden de los factores no altera el producto
\( a \cdot b = b \cdot a \)
\( 5 \cdot 3 = 3 \cdot 5 \)
2. Propiedad asociativa
El orden como se agrupen o se asocien los factores no altera el producto
\( ( a \times b ) c = a ( b \times c ) \)
\( (5 x 2) x 6 = 5 x (6 x 2 ) \)
\( 10 x 6 = 5 x 12 \)
\( 60 = 60 \)
3. Propiedad del neutro multiplicativo
Cualquier número real multiplicado por 1, es igual al número real.
\( a x 1 = a \)
\( 8 x 1 = 8 \)
4. Propiedad del inverso multiplicativo
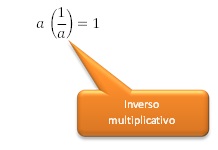
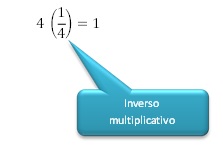
5. Propiedad distributiva
Por medio de esta propiedad podemos convertir un producto de sumas, en una suma de productos:
\( a ( b + c ) = ab + ac \)
producto → suma
\( 2 ( 4 + 5 ) = ( 2 x 4) + ( 2 x 5) \)
\( 2 x 9 = 8 + 10 \)
\( 18 = 18 \)
Comprueba tus conocimientos, haz clic en el siguiente icono