Tema 2. Funciones

Desde el punto de vista de conjuntos podemos definir a las relaciones y funciones de la siguiente manera:

Relación: Cuando a todos o algunos elementos del conjunto A le corresponde uno o varios elementos del conjunto B.

 

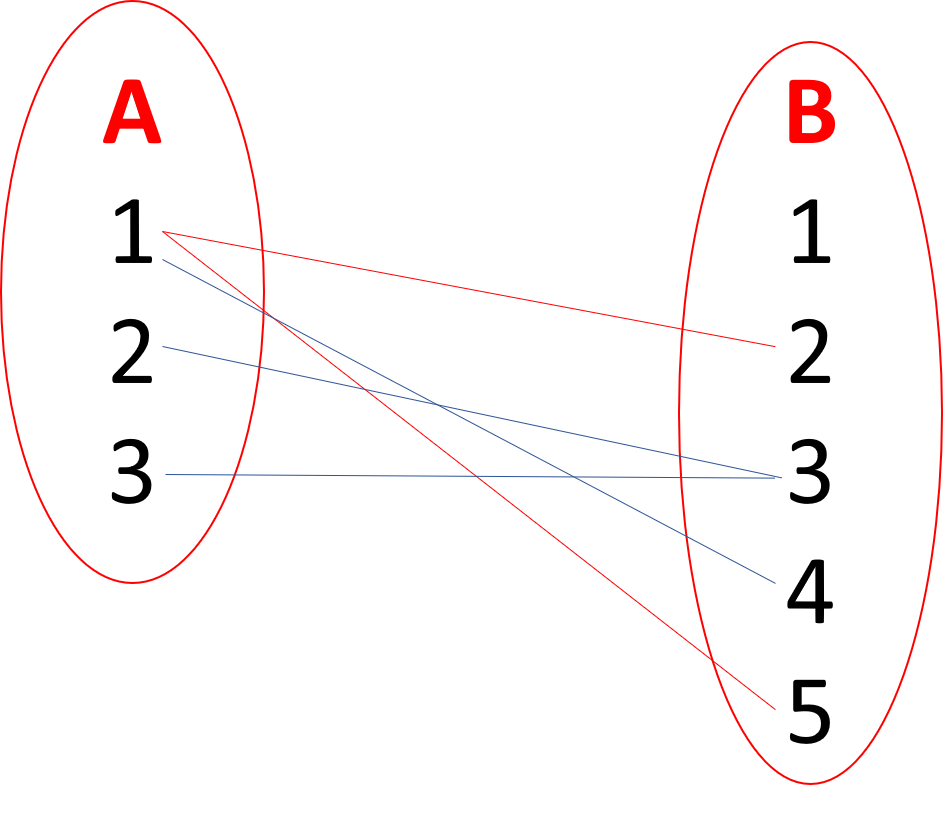
Función: Es una relación en la cual a cada elemento del conjunto A le corresponde solo un elemento del conjunto B.

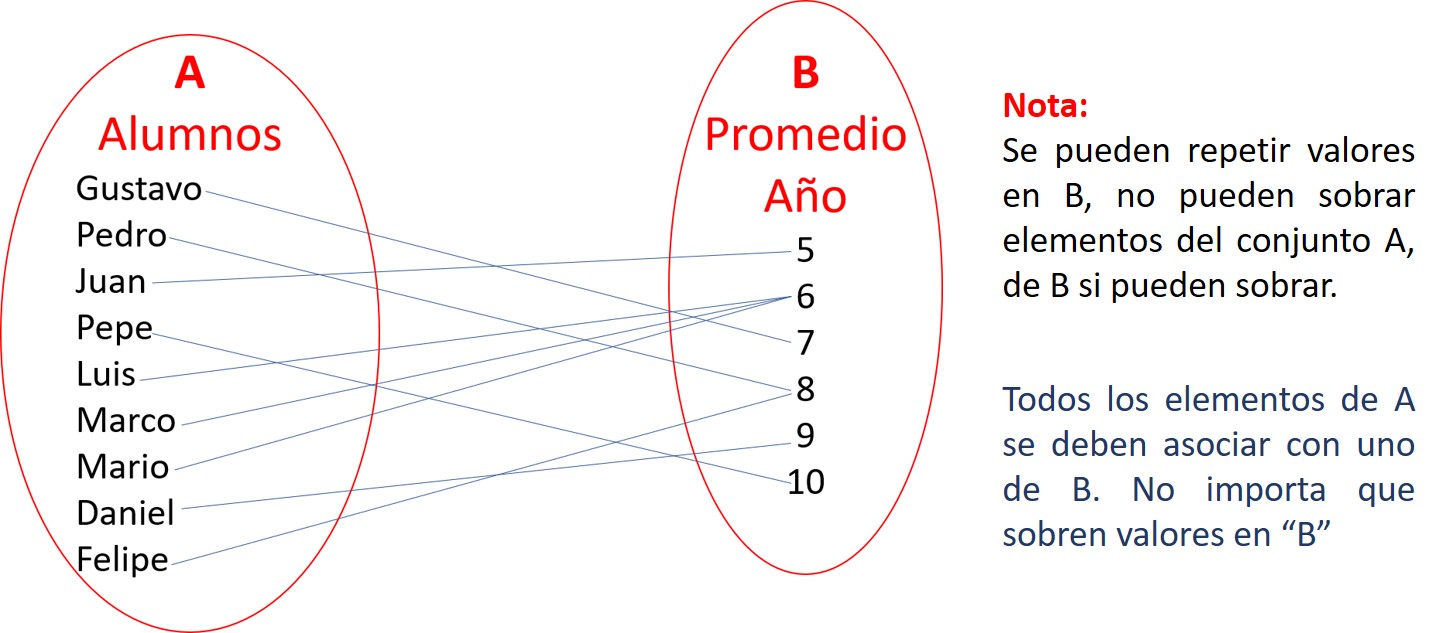
Pedro (conjunto A) solo puede tener una calificación que es 8.

Dominio, Codominio, y Rango 

Dominio: Es el conjunto formado por los primeros elementos de las parejas ordenadas. Valores permitidos por la variable "x". 

Codominio o Contradominio: Es el conjunto formado por los segundos elementos de la pareja ordenada. Generalmente, el codominio siempre son todos los reales.

Rango o Imagen: Es el conjunto formado por los segundos elementos de la pareja ordenada, después de aplicar la regla de correspondencia, es decir, la función propuesta.

Nota: Si no hay regla de correspondencia, el codominio y el rango son iguales.

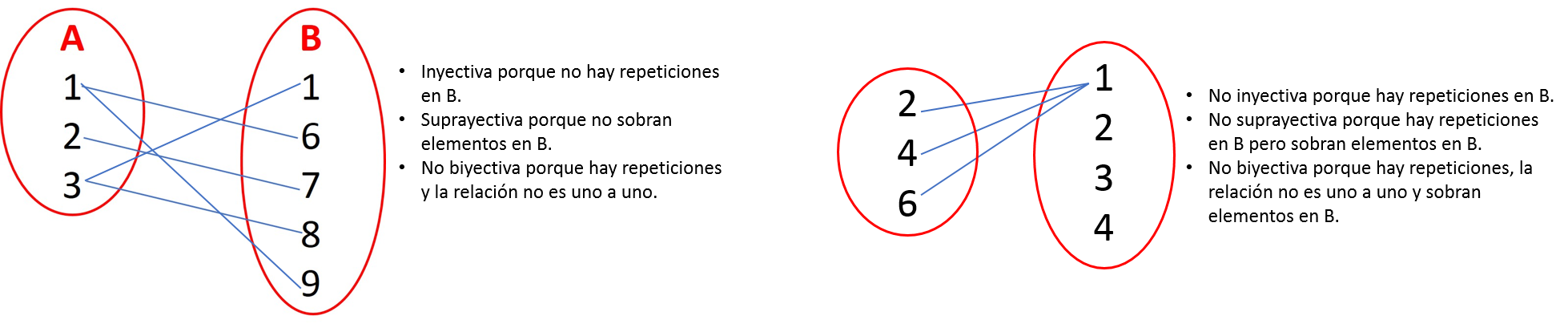
Funciones Inyectiva, Suprayectiva y Biyectiva

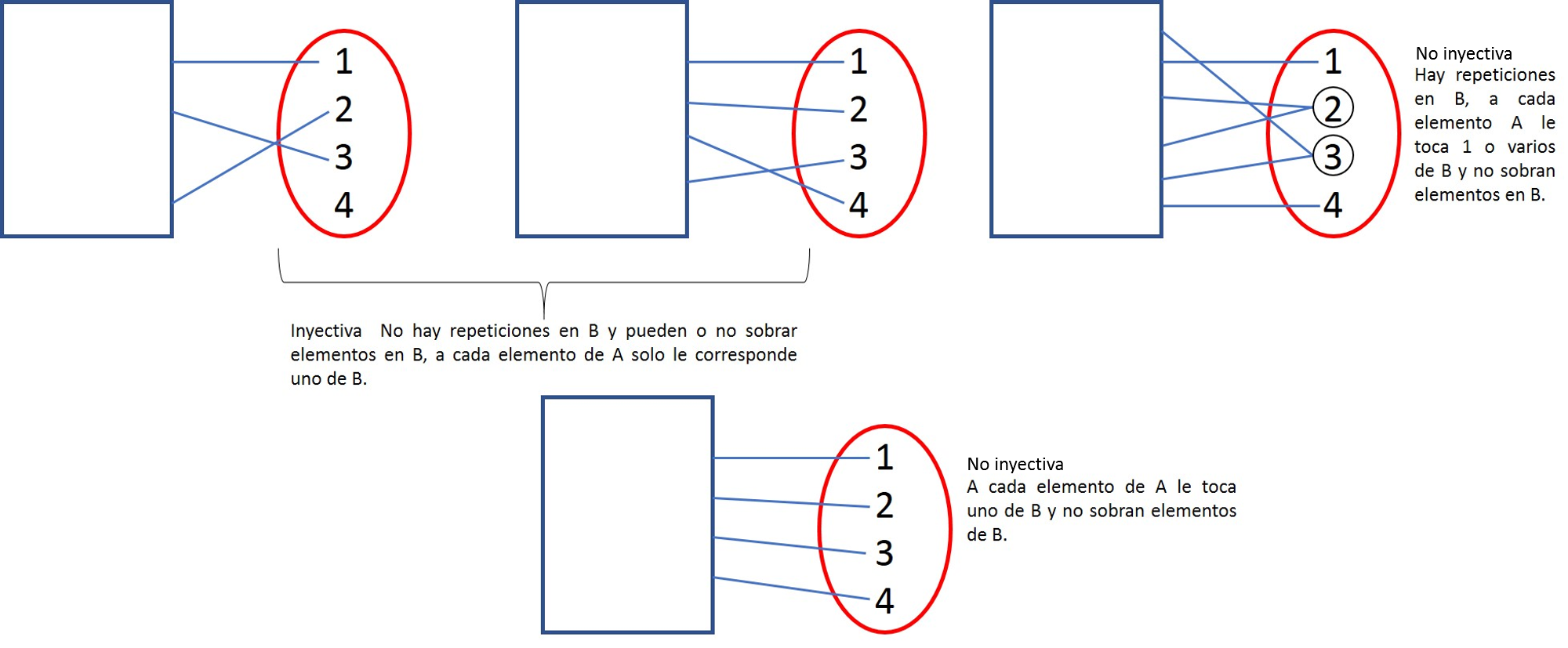
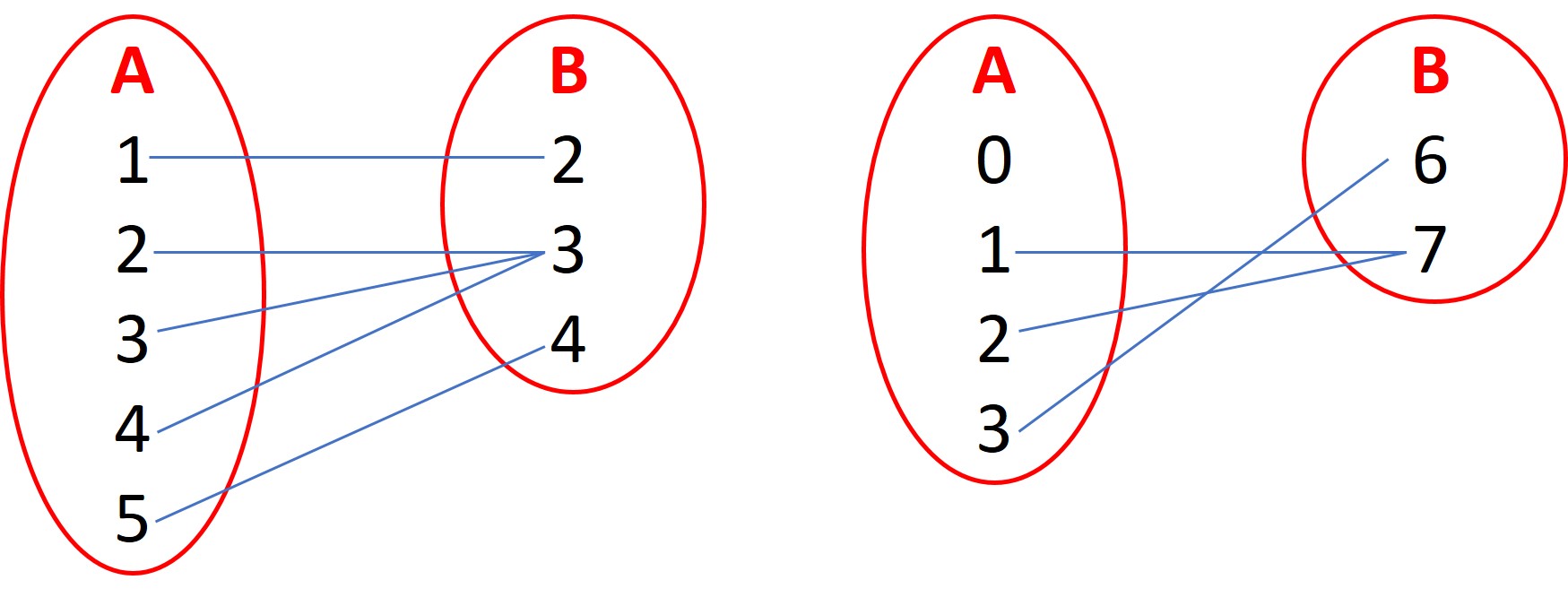
Inyectiva Una función inyectiva o unívoca es cuando a cada elemento del conjunto B , le corresponde sólo un elemento del conjunto A sin importar que sobren elementos en el conjunto B.

Una manera fácil de saber si son inyectivas es analizando solo el conjunto B y tapando el conjunto A.

Suprayectiva o Sobreyectiva

Es cuando a cada elemento del conjunto B le corresponde una o más elementos del conjunto A. No deben sobrar elementos de B y no sobran elementos del conjunto A.

Biyectiva

Cuando una función es inyectiva y a la vez y a la vez suprayectiva, entonces es biyectiva, es decir que a cada elemento de A le corresponde uno solo de B y no sobran elementos del conjunto B.

Distinguir si la función es inyectiva, suprayactiva o biyectiva