Medición Aproximada de Figuras Amorfas
La medición aproximada de las figuras amorfas consiste en una serie de métodos utilizados para determinar el área o el perímetro de figuras geométricas que no son triángulos, cuadrados, círculos, etc. Algunos son extensibles a figuras tridimensionales.
Cuando hablamos de figuras amorfas, nos referimos a aquellas formas irregulares y sin una geometría definida. Estas figuras no pueden medirse directamente con fórmulas geométricas clásicas como las que usamos para círculos, cuadrados o triángulos. Sin embargo, podemos obtener una medida aproximada del área de estas figuras utilizando técnicas como la suma de áreas de figuras más simples o métodos más avanzados como las Sumas de Riemann.
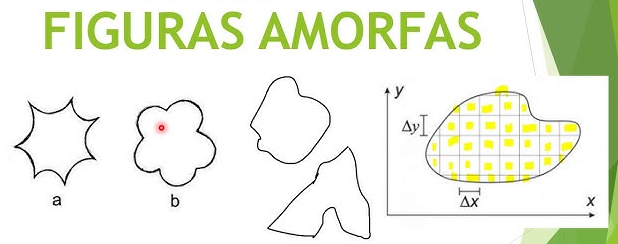
Método de Aproximación con Cuadrículas
Uno de los métodos más sencillos para aproximar el área de una figura amorfa es usar una cuadrícula superpuesta sobre la figura y contar los cuadrados completos e incompletos que caen dentro de la figura. Este método es una aproximación, pero es útil para obtener una idea razonable del área.
Ejemplo Paso a Paso
Imaginemos que tenemos una figura amorfa dibujada sobre una cuadrícula donde cada cuadrado mide 1 unidad por 1 unidad.
Paso 1: Superponer una cuadrícula sobre la figura
Dibujamos una cuadrícula sobre la figura amorfa. La idea es que la cuadrícula esté alineada de modo que los cuadrados cubran toda la figura.
Paso 2: Contar los cuadrados completos dentro de la figura
Empezamos por contar cuántos cuadrados completos están completamente dentro de la figura amorfa. Supongamos que contamos 6 cuadrados completos.
Paso 3: Contar los cuadrados parcialmente dentro de la figura
Luego, contamos los cuadrados que están parcialmente dentro de la figura. Para obtener una mejor aproximación, podemos sumar estos cuadrados como fracciones. Por ejemplo, si 5 cuadrados están medio llenos, podemos sumar 2.5 unidades de área.
Paso 4: Calcular el área total aproximada
Sumamos el número de cuadrados completos y las fracciones de cuadrados parciales para obtener el área aproximada de la figura.
En este ejemplo:
- Cuadrados completos: 6
- Cuadrados parciales (suma de fracciones): 2.5
Área aproximada = 6 + 2.5 = 8.5 unidades cuadradas
Uso de las Sumas de Riemann
Si la figura es más compleja y se puede aproximar usando una curva o función matemática, podemos aplicar Sumas de Riemann. Este método divide el área bajo una curva en rectángulos y suma sus áreas. Al aumentar el número de rectángulos, la precisión de la aproximación mejora.